J'ai trouvé un bug dans Python !

J’ai trouvé un bug qui affecte toutes les versions récentes de Python, et il est interdit de le réparer ! Voici pourquoi.

Comme pour de très nombreux langages de programmation, le générateur de nombres aléatoires intégré à Python porte le nom de Mersenne Twister, ou MT19937.

C’est un RNG (Random Number Generator) très rapide et qui offre une entropie de très bonne qualité.

Mais le MT19937 n’est pas sécurisé contre les attaques cryptographiques : comme tous les générateurs de nombres aléatoires, il n’est en réalité que pseudo-aléatoire : après l’initialisation de ses variables internes, les bits en sortie sont produits de manière déterministe.

Si un attaquant parvient à récupérer environ 20 kilobits consécutifs produits par une instance de Mersenne Twister, il peut reconstituer l’état de la mémoire interne du générateur, et peut ainsi prédire tous les nombres suivants qu’il produira.

Cette vulnérabilité est bien connue, et c’est pour ça qu’il faut absolument utiliser un RNG dit “cryptographique” si l’on souhaite avoir des nombres aléatoires vraiment imprévisibles, par exemple pour le tirage sur des casinos en ligne ou la génération de mots de passe.

En 2019 alors que j’étais en pleins préparatifs pour le CTF INS’hAck (Capture The Flag = compétition de cybersécurité ), je voulais crééer un challenge de crypto sur lequel les participants devraient mettre en oeuvre une attaque contre le générateur MT19937 de Python.

En général, les challenges qui demandent une attaque sur Mersenne Twister on les voit venir de loin : comme il faut récupérer 624 sorties consécutives de 32 bits pour pouvoir réaliser l’attaque, on voit très souvent “random.getrandbits(32)” dans le code source à exploiter.

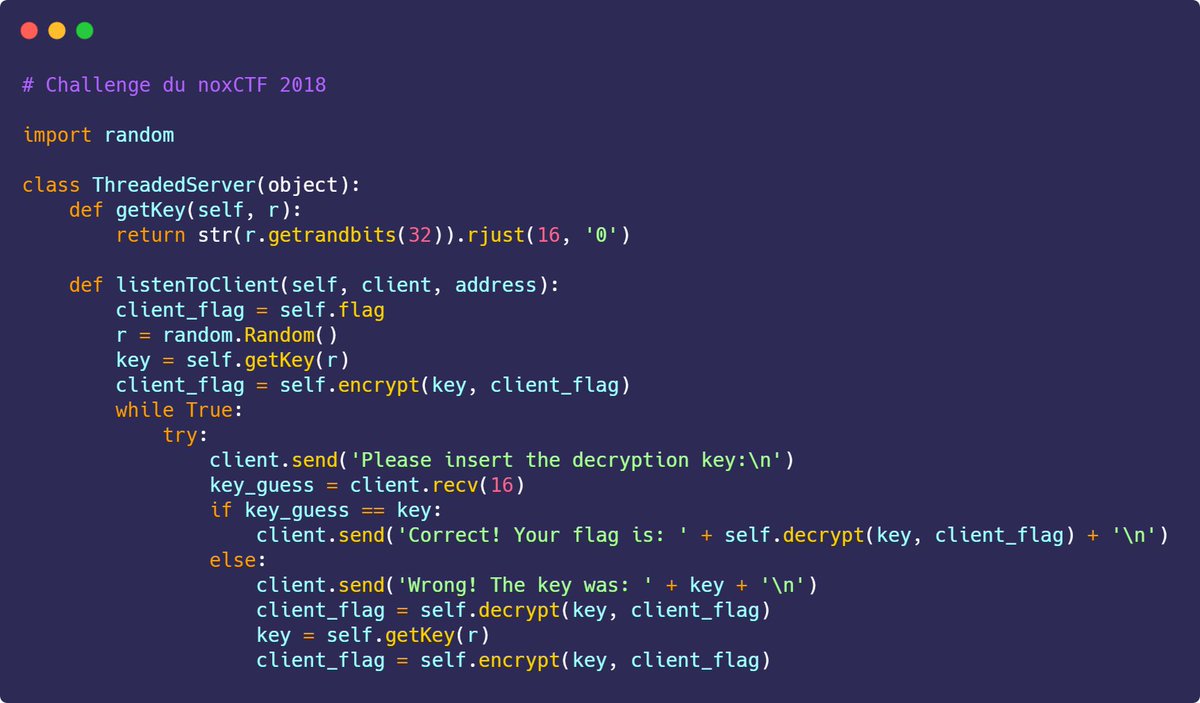
Moi, j’avais envie de le déguiser un peu mieux que ça, pour que la porte dérobée soit moins évidente : il existe plein d’autres fonctions qui génèrent des bits aléatoires et qui sont bien plus souvent utilisées dans le monde réel : randint, shuffle, randrange, sample, etc.

Par exemple, saviez-vous que pour mélanger de manière parfaitement uniforme une liste de longueur N, il suffit de O(N) opérations ? On commence par choisir un index entre 0 et N-1, avec lequel on échange l’élément à l’indice N-1. Pareil pour N-2, et ainsi de suite jusqu’à 1.

C’est ce genre d’opération que je voulais utiliser dans mon code source vulnérable, les joueurs devraient alors étudier le fonctionnement interne de l’interpréteur Python pour comprendre comment retrouver les bits d’entropie au lieu de leur donner gratuitement avec getrandbits.

Un très grand nombre de fonctions du module random de Python font appel à la fonction cachée _randbelow, qui gère les appels au générateur de bits aléatoires du Mersenne Twister. Sa seule utilité est, comme son nom l’indique, de renvoyer un nombre entier compris entre 0 et n-1.

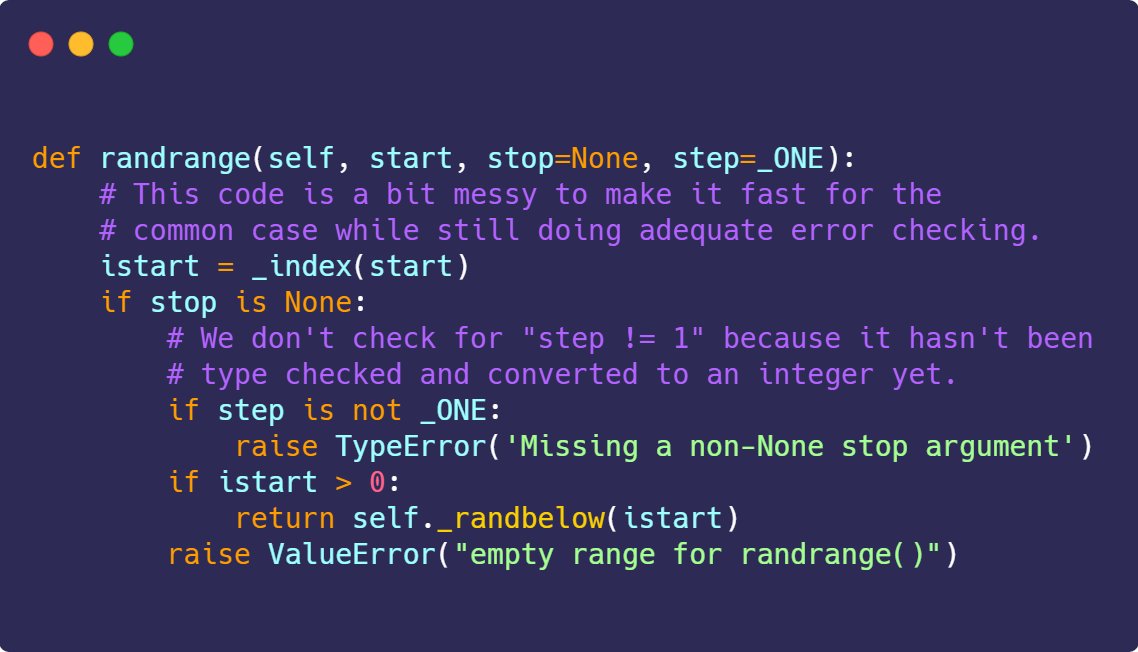
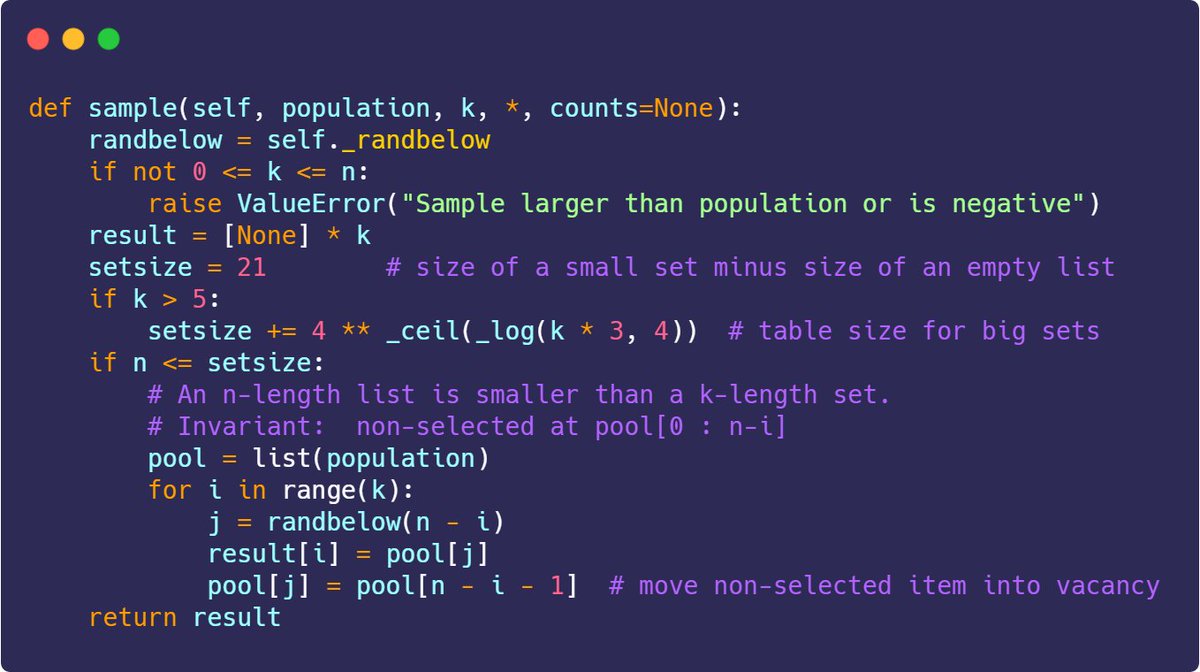
Du coup, à partir d’un résultat donné d’une fonction shuffle/randint/sample on devrait pouvoir retrouver le résultat des différents appels à randbelow, et à partir de ceux-ci tous les bits qui ont été produits par getrandbits. C’est simple non ? Ben en pratique pas tant que ça 😉

Pour comprendre comment fonctionne randbelow, il faut d’abord que je vous parle de la méthode de sélection/rejet qui est utilisée pour simuler des tirages sur n’importe quelle loi de probabilités. Admettons par exemple que vous souhaitiez choisir un point au hasard sur un disque:

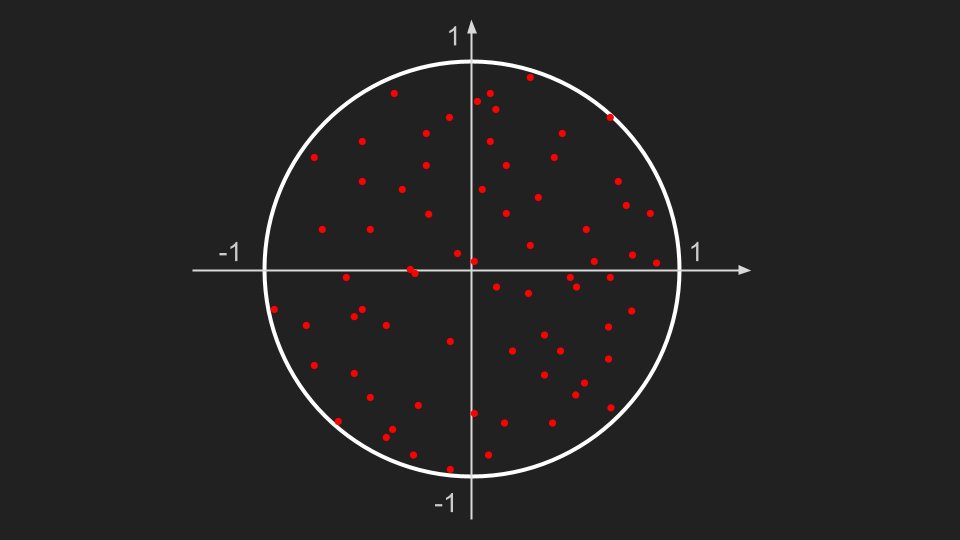
On peut par exemple choisir une coordonnée x aléatoire entre -1 et 1 puis une coordonnée y aléatoire entre -sqrt(1 - x²) et sqrt(1 - x²) qui nous garantit que le point tiré sera forcément dans le cercle.

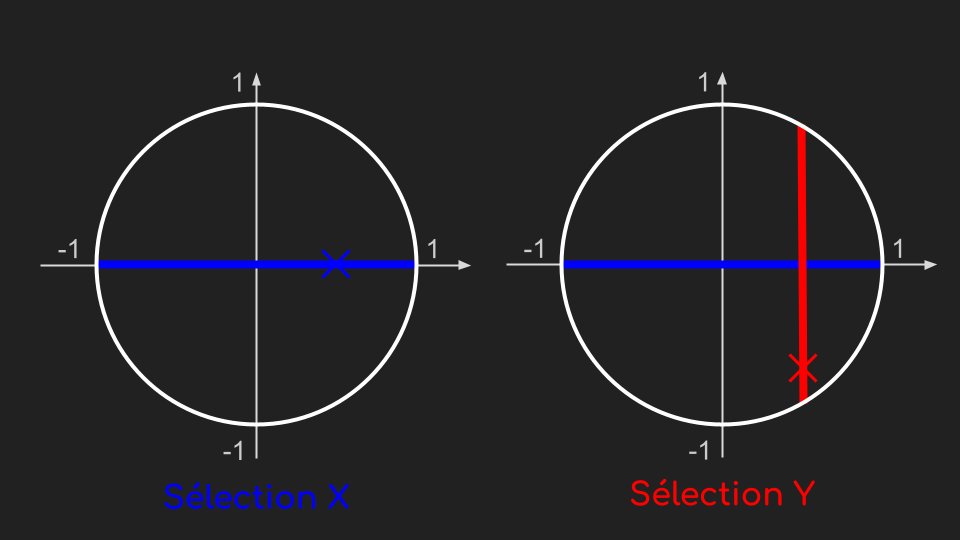
Cependant, on va rencontrer un problème : on a ici autant de chances de tomber dans la zone bleue que dans la zone jaune, alors que celles-ci ont des aires différentes : la densité du tirage n’est pas uniforme !

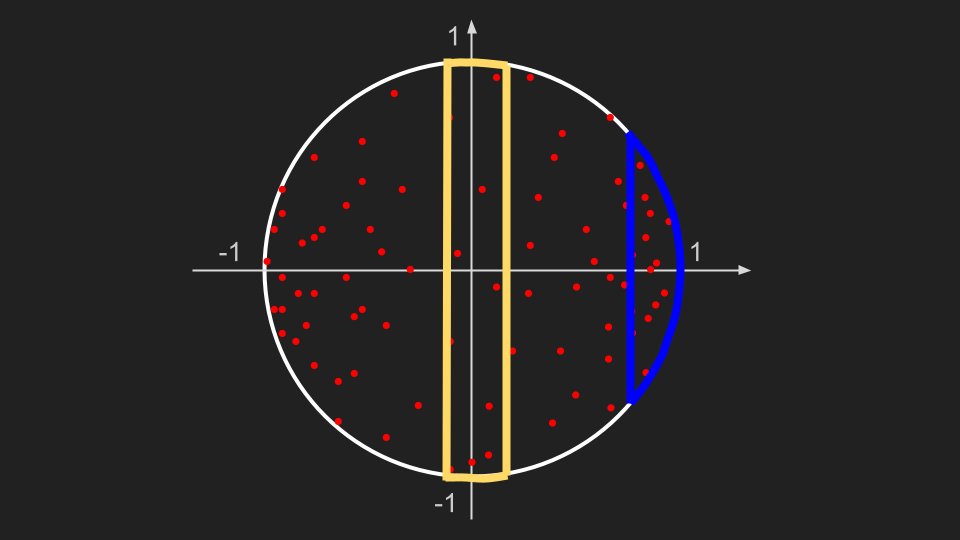
La méthode par rejet permet quant à elle de faire des tirages aléatoires compliqués en se basant un générateur de nombres aléatoires simple. On peut par exemple partir du carré, sur lequel il est facile de générer des points uniformes en tirant indépendamment X et Y dans [-1, 1].

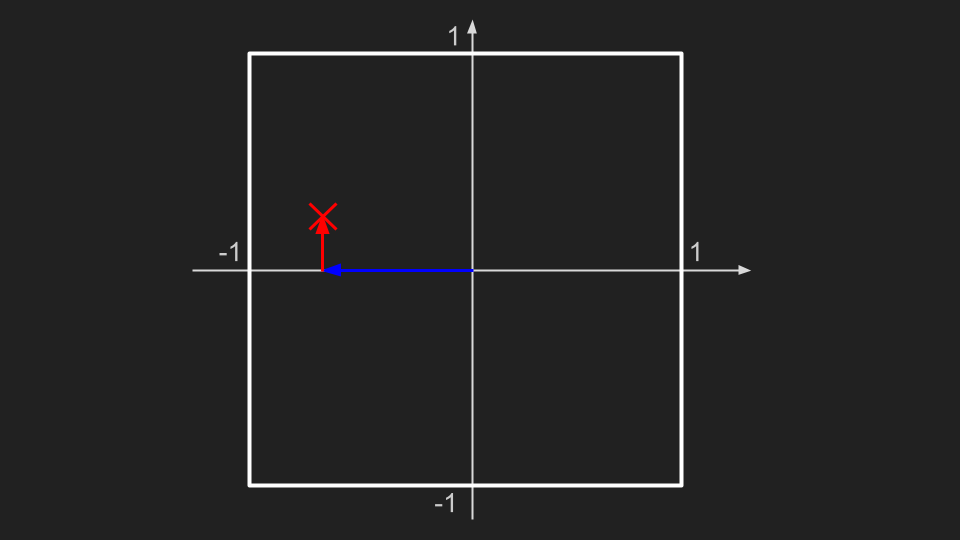
On commence donc par tirer un point au hasard uniformément dans le carré, puis on regarde si ce point est dans le disque.

Si c’est le cas, on a notre point aléatoire sur le disque, et sinon on recommence. Normalement, il suffit de quelques itérations pour trouver un point valide.

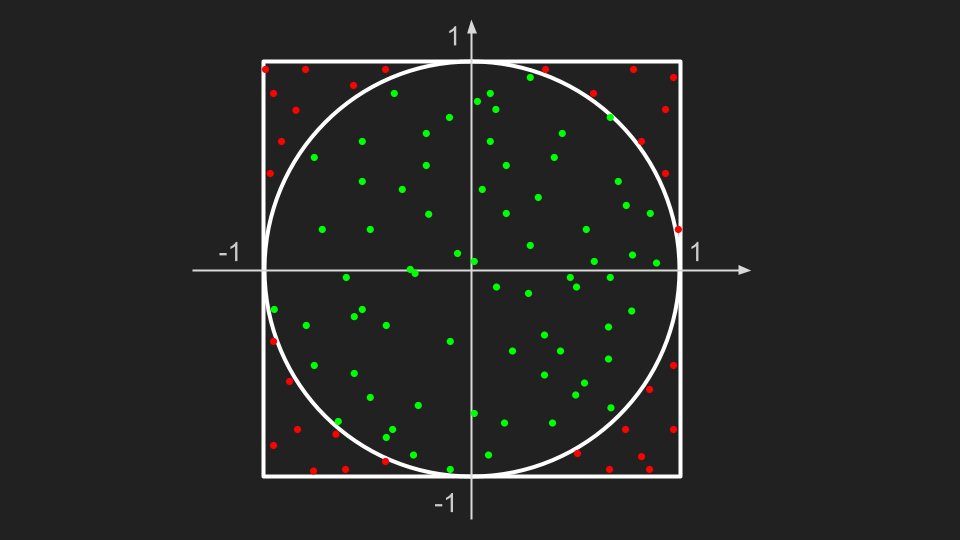
Pour le cercle il existe d’autres méthodes n’utilisant pas de rejet (avec des coordonnées polaires selon des distributions bien choisies notamment), mais le tirage sélection/rejet reste très souvent utilisé car très rapide (en moyenne) et peu susceptible aux erreurs de précision.

Le tirage de nombres entiers entre 0 et N-1 c’est un peu la même chose : on pourrait par exemple générer un nombre de 1000 bits et prendre son modulo N, mais ce n’est pas parfaitement équiprobable si le nombre n’est pas un multiple de N.

De même, on peut se dire que la fonction random (qui génère un nombre réel entre 0 et 1) peut nous aider : la partie entière de random()*N est théoriquement uniforme sur les entiers de 0 à N-1. Mais comme la représentation des flottants n’est pas continue en pratique, même souci.

Pour assurer un tirage le plus uniforme possible, Python va ainsi utiliser la méthode par rejet : à l’aide de la fonction getrandbits, il génère un entier codé sur autant de bits que notre nombre N. Tant que le nombre tiré n’est pas dans [0, N-1], on en génère un nouveau.

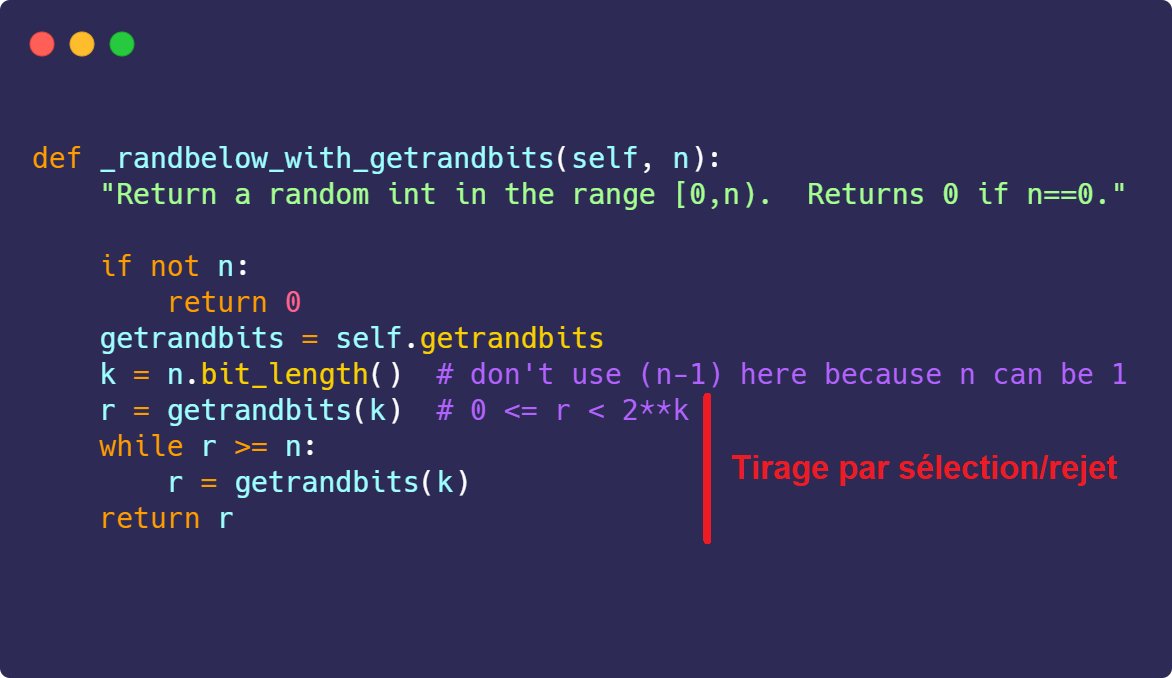
Les tirages par rejet peuvent entraîner un “gâchis” d’entropie : si le nombre tiré ne respecte pas le critère de sélection, les bits utilisés pour sa génération sont perdus. Pour mon challenge de CTF, il fallait du zéro déchet pour que l’attaquant puisse récupérer tous les bits.

Il existe un seul cas dans lequel _randbelow serait garanti de ne faire qu’un seul tirage : si N est une puissance de 2, alors n’importe quel nombre tiré avec getrandbits() est dans [0, N-1] et il n’y a pas de rejet. Sauf que j’ai trouvé un bug dans l’implémentation de Python !

Pour calculer le nombre de bits à tirer aléatoirement, on va appeler la fonction n.bit_length(). Dans le cas où N est une puissance de deux, ce nombre de bits est incorrect : en prenant n=1024 (2^10), on ne devrait à avoir à tirer que 10 bits. Cependant, n.bit_length() vaut 11 !

Par conséquent, au lieu d’avoir un tirage parfait qui consomme exactement le bon nombre de bits et réussit du premier coup, on se retrouve avec des tirages qui n’ont que 50% de chances de réussir, et qui utilisent en moyenne 2 fois trop de temps et d’entropie. Du coup, je me suis mis en tête de proposer un patch du code source de Python.

Comme pour tout projet titanesque, la procédure est assez lourde : il faut créer une issue détaillée sur le tracker externe, signer un accord de propriété intellectuelle, compiler et tester le fork, …

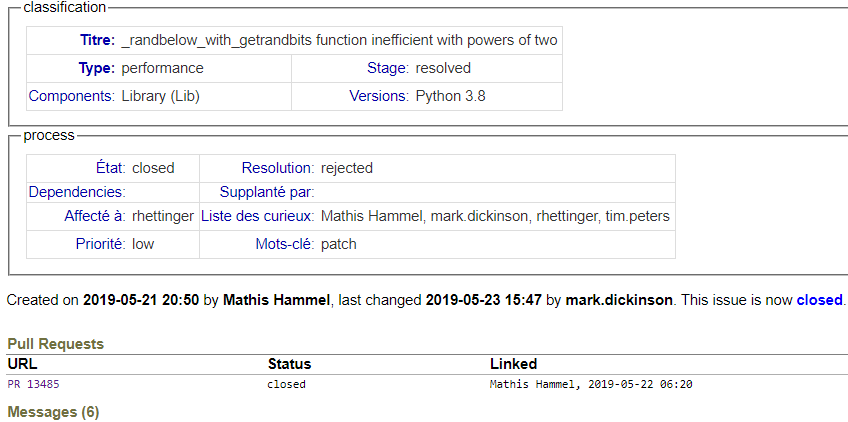
Avec une modification de seulement 4 lignes de code, mon fork fonctionne bien et on observe une accélération effective de 2x sur les appels à _randbelow sur les puissances de 2. Victoire !

Mais petit souci : y a des dizaines de tests unitaires qui ne passent pas !

En effet, le module random de Python doit respecter la reproductibilité : pour une même seed, le RNG devrait produire exactement les mêmes résultats entre toutes les versions de Python. Mais ce n’est pas le cas ici parce qu’on a réparé les fuites d’entropie !

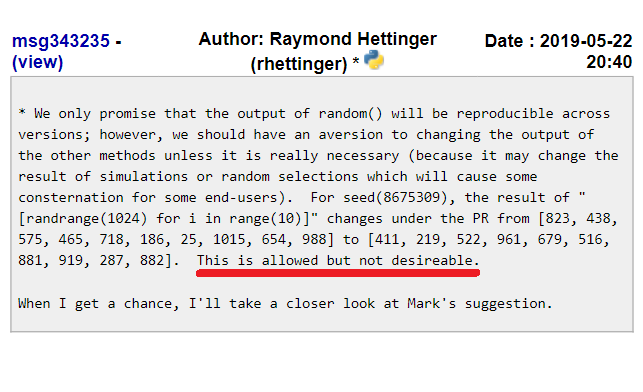
Pour conclure, ce bug assez spécifique ne permet pas de justifier un tel changement, et le bug devra donc rester éternellement dans Python. Mais ça n’a pas été peine perdue, le bug que j’ai ouvert a engendré un refactoring et un nouveau fonctionnement interne à getrandbits :)

Voilà, j’espère que cet article vous a plu et que vous saurez briller en société avec vos nouvelles connaissances sur les tirages par sélection/rejet et sur les internals de Python ;)