Non, ChatGPT n'est pas devenu nul en maths
ChatGPT est-il devenu nul en maths ? Cette affirmation, basée sur une é...
Un programme de 15 lignes de code Python arrive à rivaliser avec les meilleures intelligences artificielles !
Cette drôle de découverte vient d’être publiée par une équipe de chercheurs canadiens, et risque de bouleverser le monde du Machine Learning.
Explications ⤵️

La classification de texte est l’un des domaines de recherche les plus actifs en intelligence artificielle : elle consiste à trier automatiquement des textes courts dans un ensemble de catégories pré-définies.

Pour évaluer la performance d’un modèle, on va travailler avec des datasets spécifiques.
L’un des plus connus est basé sur 1.4 millions de questions posées sur le site Yahoo Answers, réparties en 10 catégories :
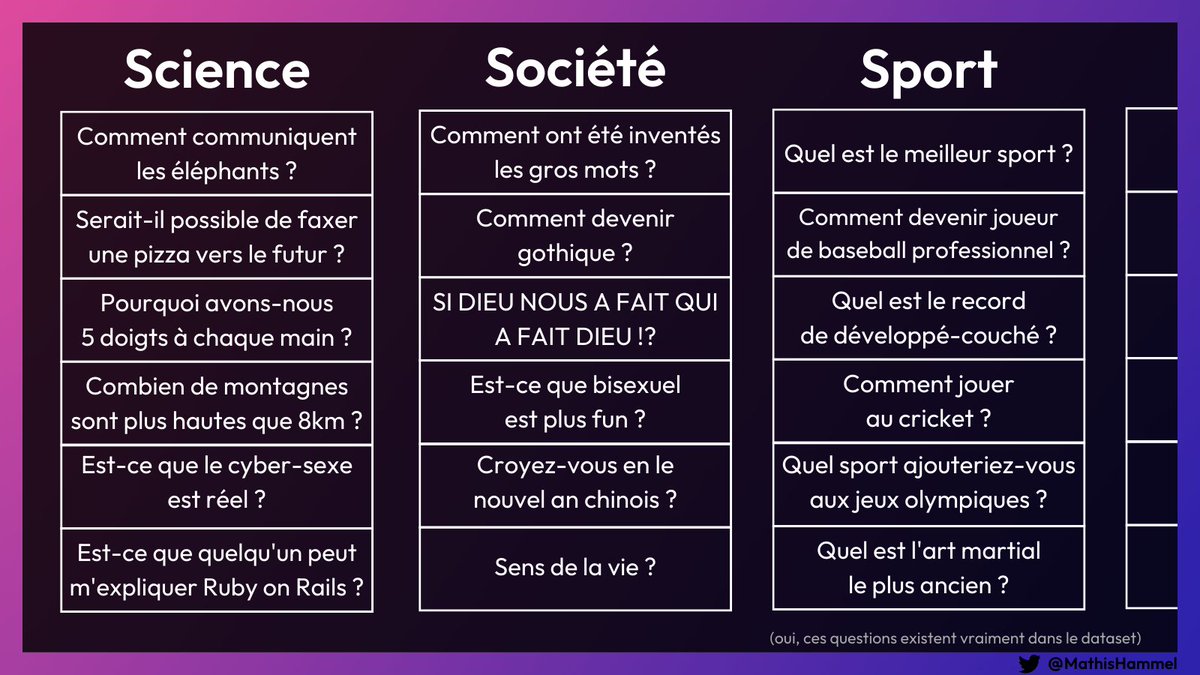
L’algorithme peut donc utiliser ces données pour apprendre à quoi ressemblent les questions de chaque catégorie.
On va ensuite le mettre à l’épreuve avec 60 000 questions non-étiquetées sur lesquelles il devra prédire la catégorie.

Il existe plusieurs manières de mesurer la performance d’un modèle de machine learning sur cette tâche.
La plus courante consiste à simplement calculer le taux de prédictions correctes : par exemple, un modèle qui donne 45k catégories correctes sur les 60k textes aura un score de 75%.
Cette mesure est appelée l’accuracy, ou “précision” en français.
Cependant, le mot français est peu utilisé car ambigu avec le terme anglais “precision” :
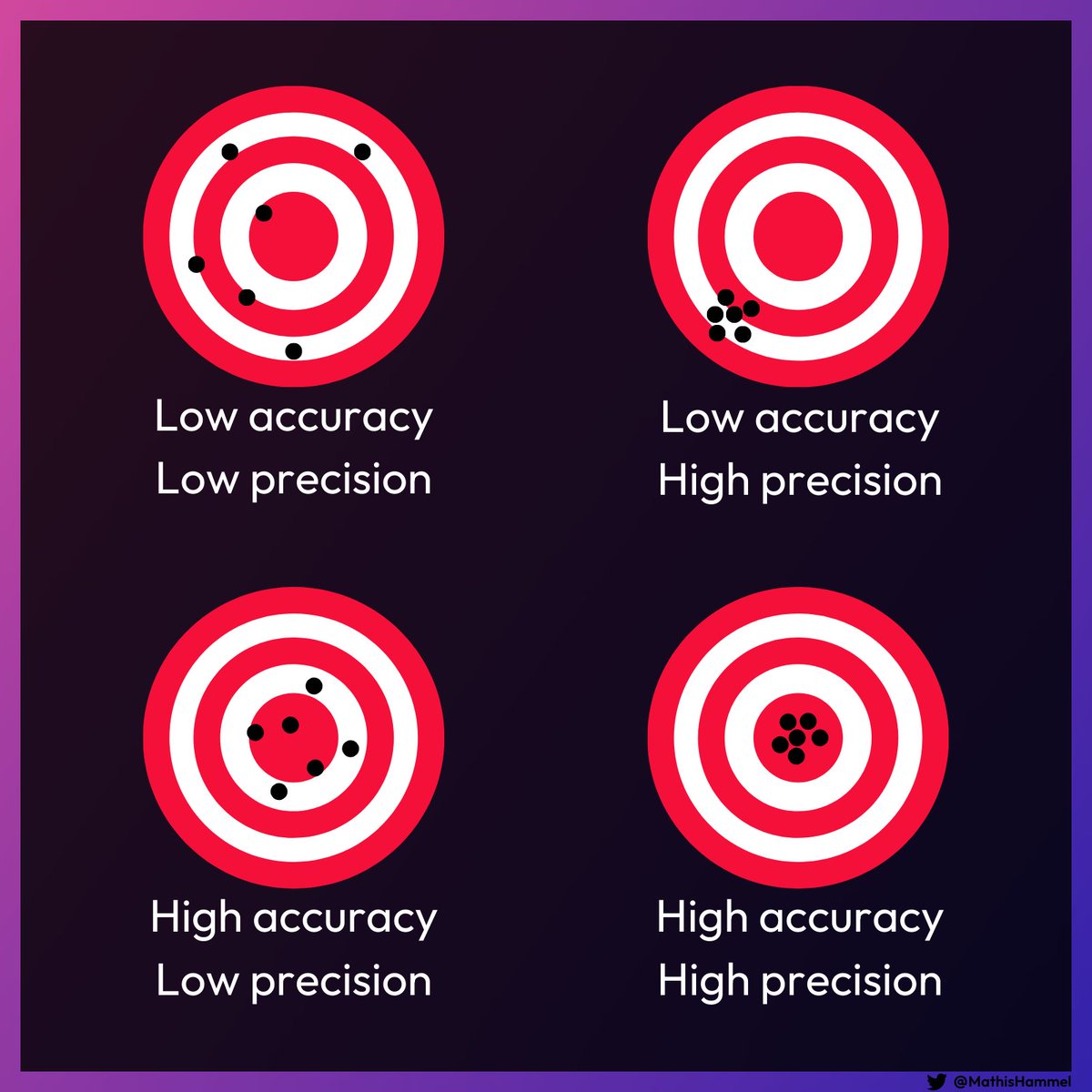
À l’heure actuelle, parmi les modèles textuels les plus performants (dits “à l’état de l’art”) on retrouve notamment BERT, publié en open source par Google en 2018.
C’est un modèle immense qui compte jusqu’à 340 millions de neurones !
Face à ce titan, les chercheurs de l’université de Waterloo ont donc décidé de créer… un script tout simple de 15 lignes. Et ça a marché 😁
Regardons de plus près son fonctionnement.
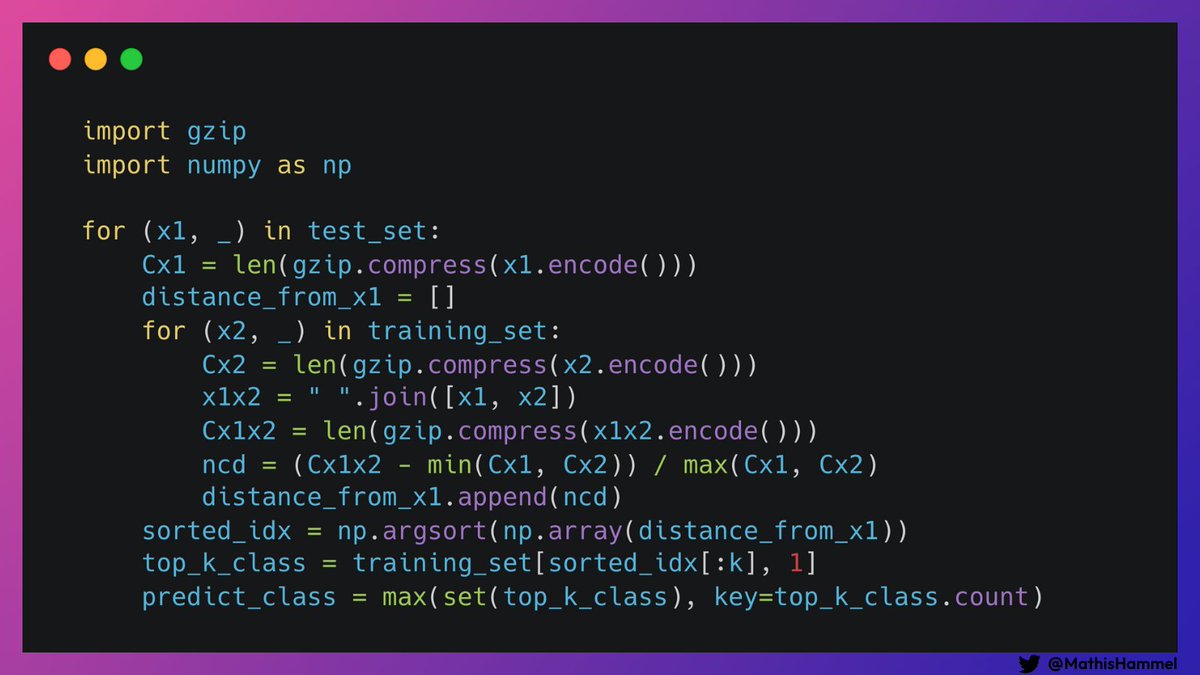
Dans l’algo présenté, on repère quelques opérations de la forme len(gzip.compress(x)) : c’est ici que se cache son secret.
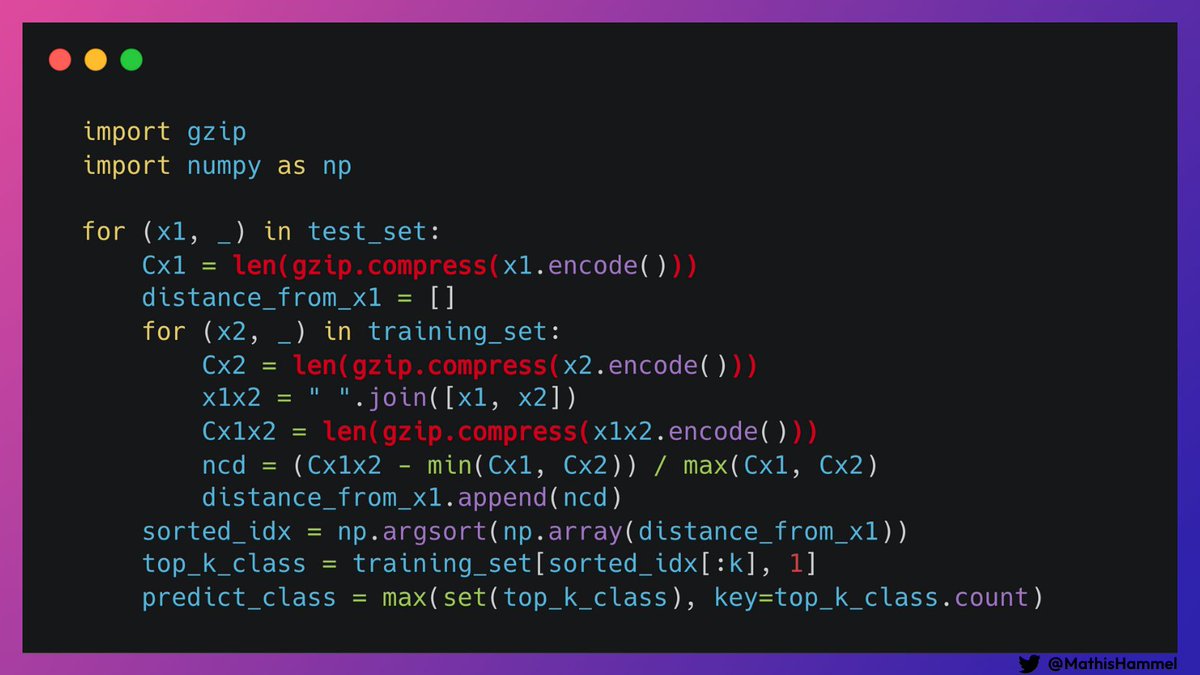
Gzip est un utilitaire de compression de fichiers basé sur le même algorithme que pour les fichiers .zip : en trouvant des motifs qui se répètent dans les données à compresser, on va pouvoir réduire la taille du fichier sans perdre d’information.
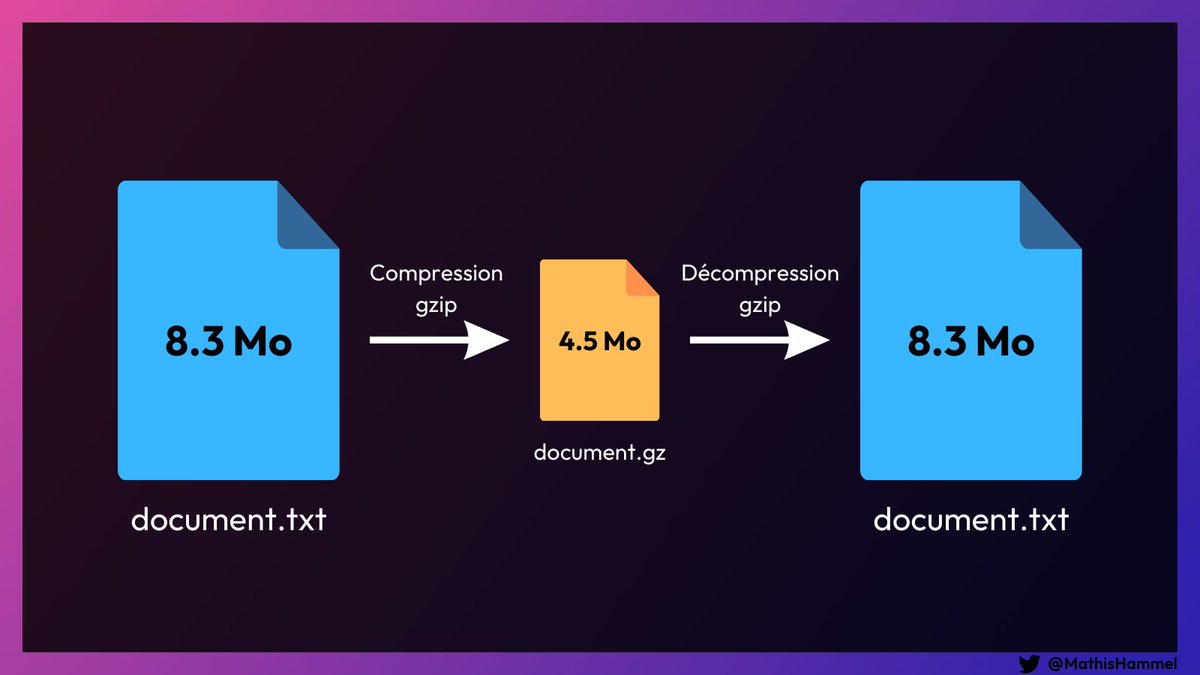
Et ce facteur de compression peut justement être utilisé pour mesurer la redondance d’information dans un texte !
J’ai compressé 1000 caractères de la page Wikipédia “réseaux de neurones artificiels” et 1000 caractères aléatoires, voici les résultats respectifs :
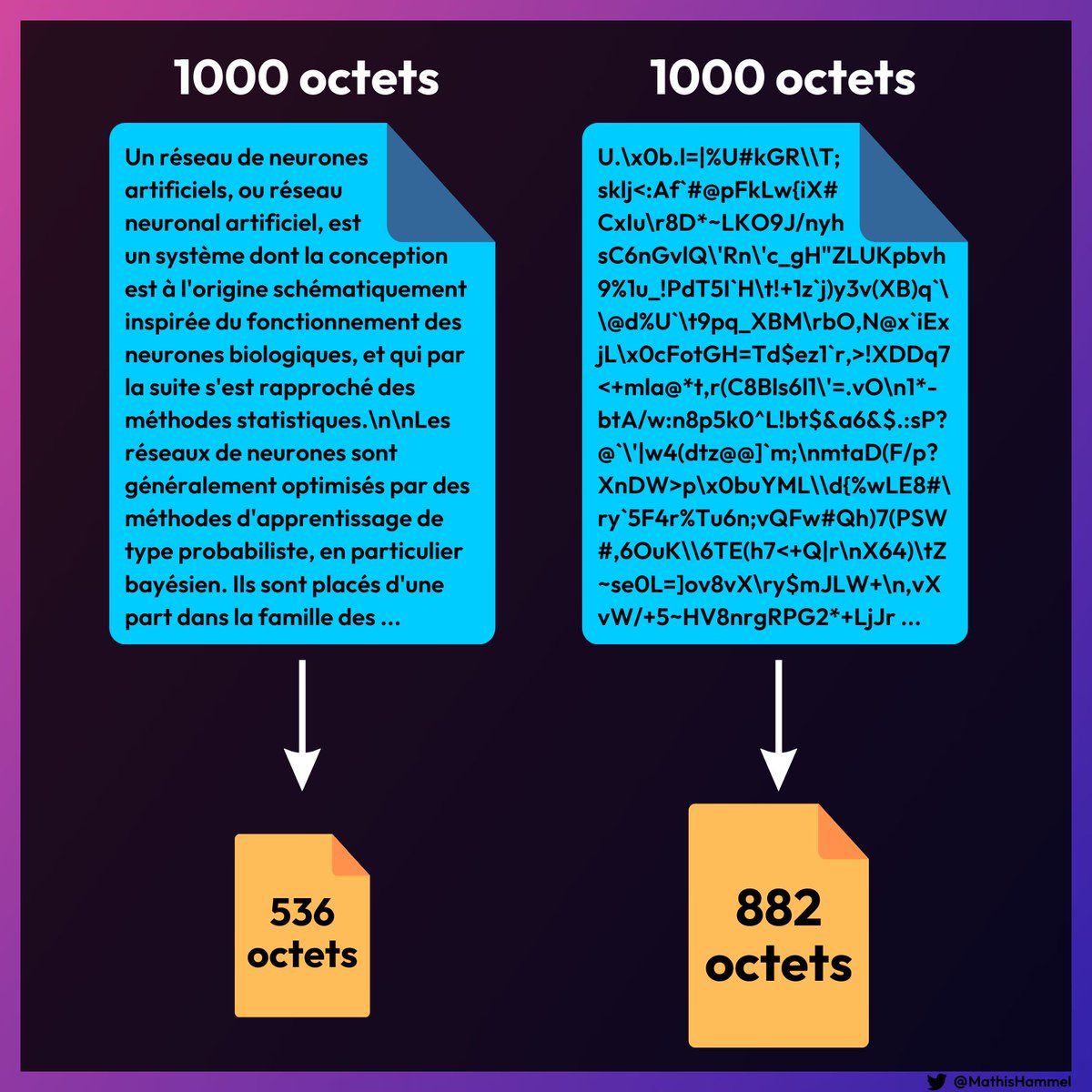
On peut donc constater qu’un texte en français contient davantage de redondance (= moins d’entropie) qui permet de le compresser plus efficacement.
De même, la concaténation de deux textes se compressera plus facilement si les deux textes sont similaires :
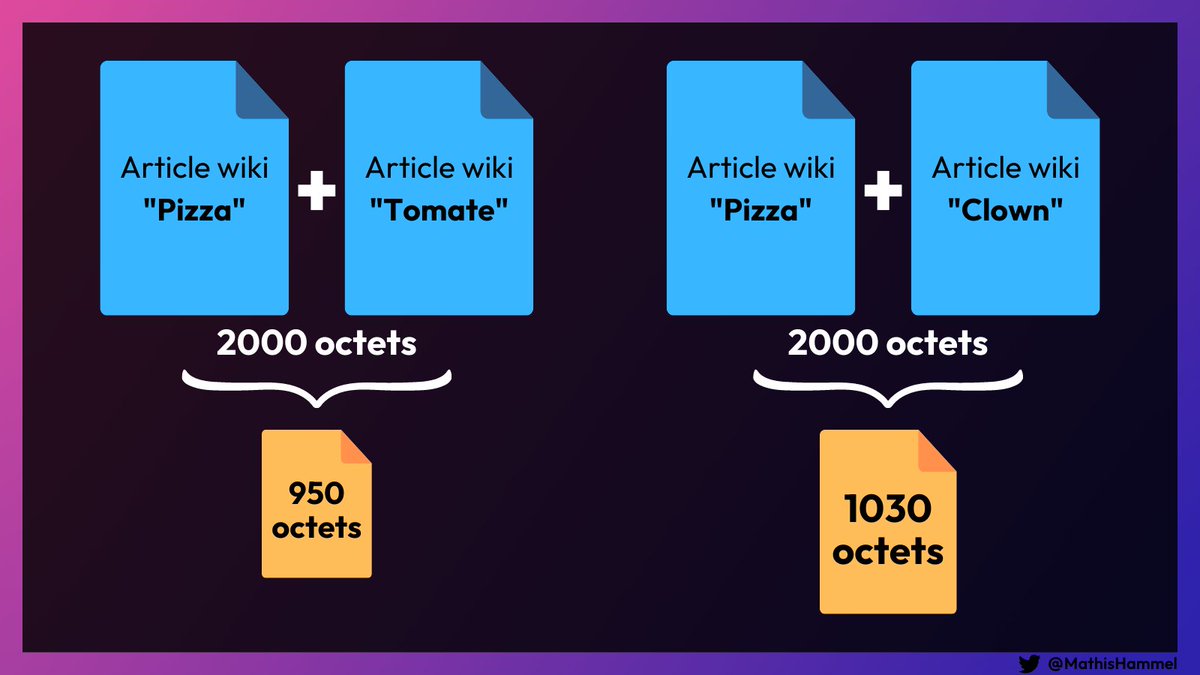
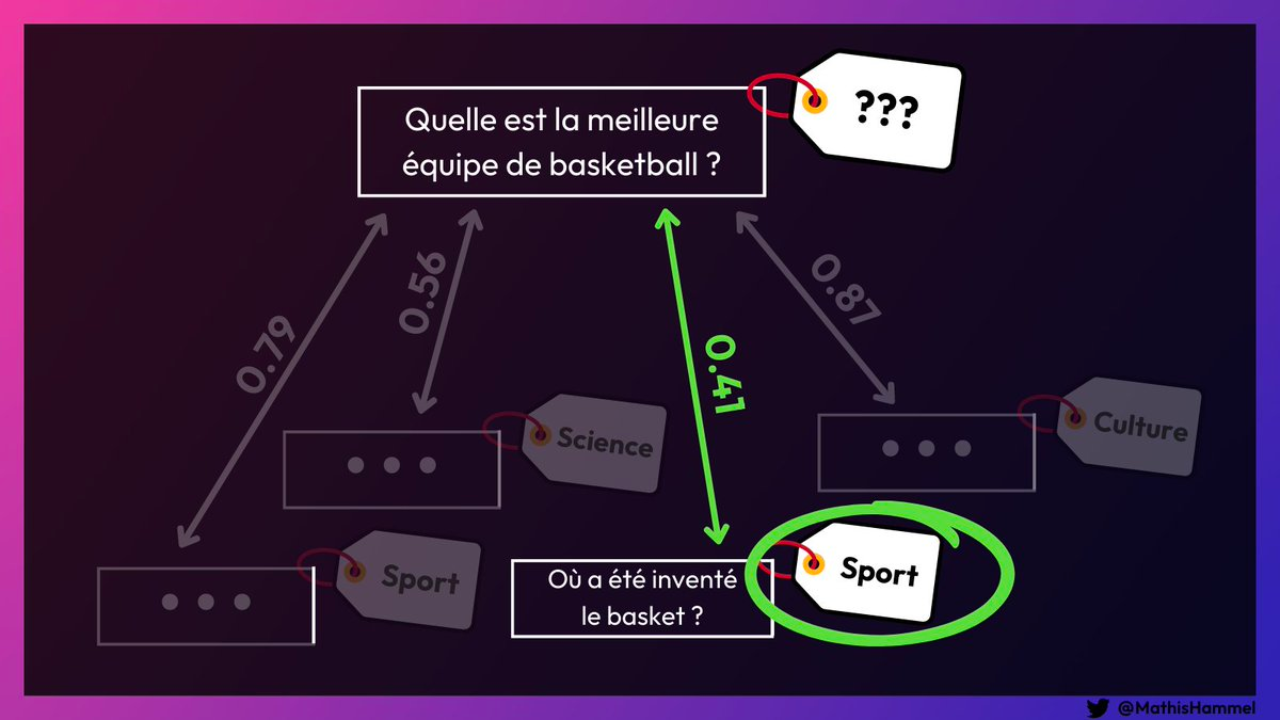
En se basant sur cette observation, on peut donc mettre en place un système capable de calculer une sorte de “distance sémantique” entre deux textes !
La formule ci-dessous est celle qui est utilisée par les chercheurs dans leur article :
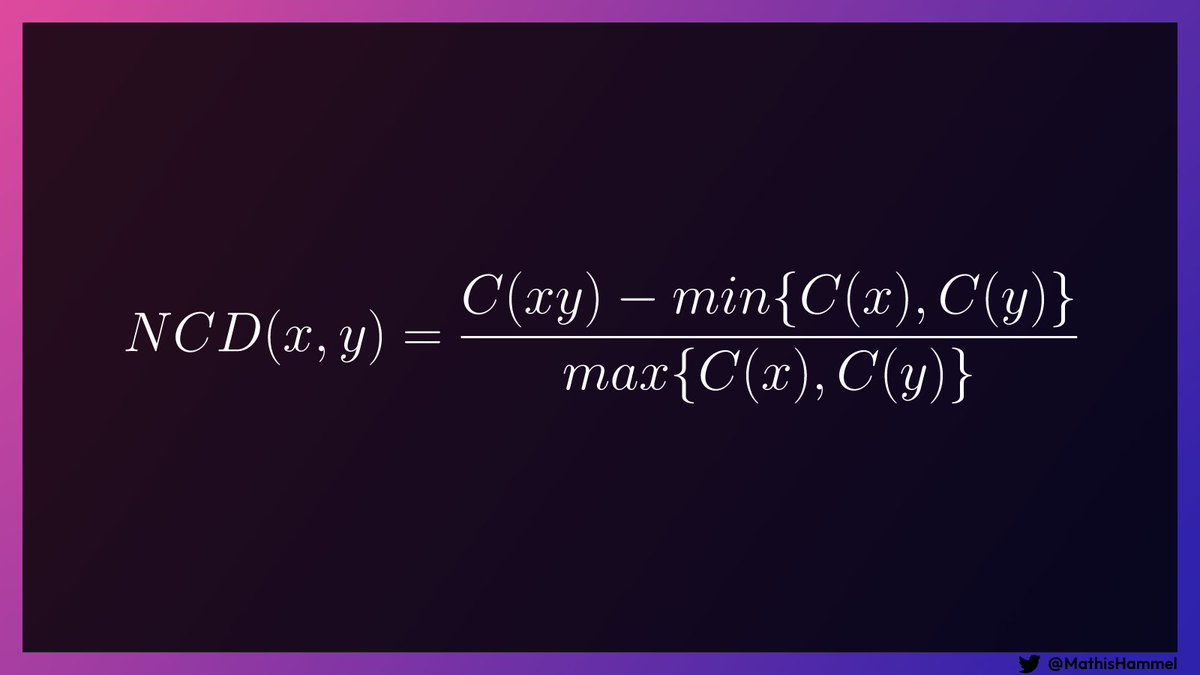
Cette formule provient de concepts théoriques comme la distance de Kolmogorov conditionnelle et l’information algorithmique mutuelle.
Sûrement des concepts inventés par les chercheurs pour se la péter en soirée, mais je vais vous montrer qu’on peut la comprendre facilement.

Considérons que l’on veut comparer la similarité de deux textes x1 et x2. On note C(x) la taille d’un texte x après compression.
Pour simplifier les choses, on va dire que la distance est comprise entre 0 et 1, et que C(x1)≥C(x2).
Penchons-nous sur deux cas extrêmes :
x1 et x2 sont extrêmement similaires : les infos de x2 sont entièrement contenues dans x1.
Ajouter x2 après x1 ne change pas la taille du fichier compressé.
Les deux textes sont très proches, on souhaite donc que leur distance soit 0.

x1 et x2 sont radicalement différents : compresser x1+x2 ensemble ne permettra pas de gagner de place par rapport à la compression des deux textes séparément.
Ici, on veut donner une distance élevée (donc 1) à cette paire de textes.

Bien sûr, ces deux cas sont extrêmes et ne se produisent pas en pratique, mais à l’aide de ces deux points de référence il est maintenant possible de mettre en place une fonction affine qui donne la distance en fonction de C(x1+x2) :
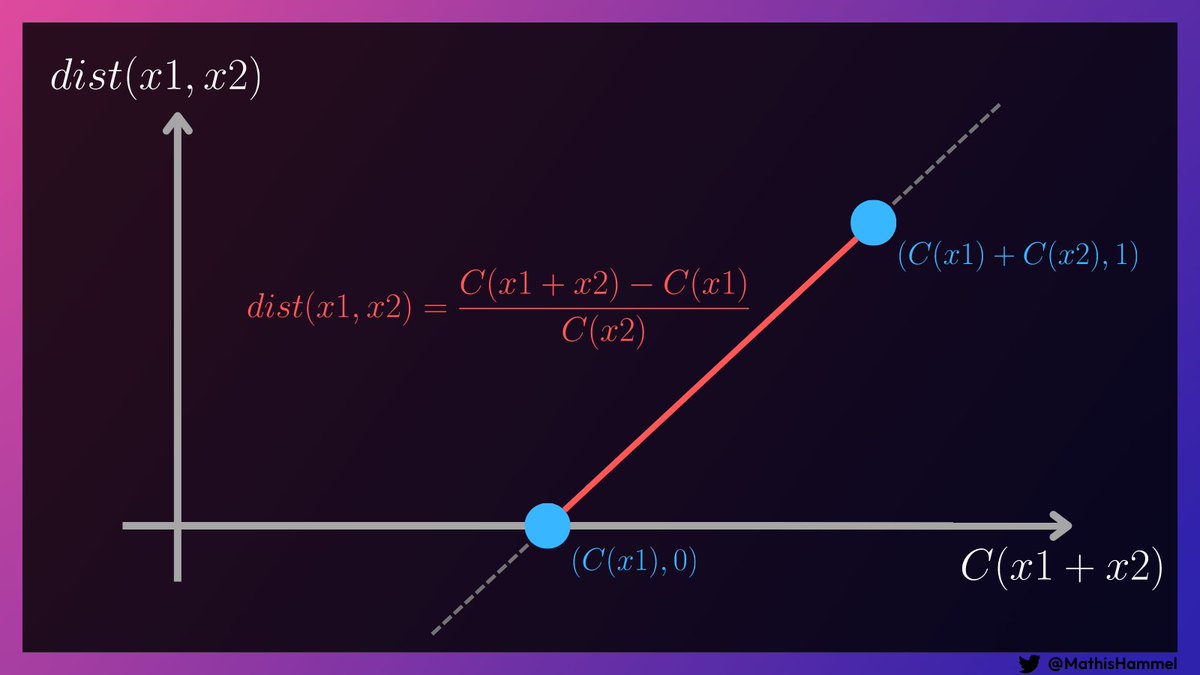
L’équation de la droite ci-dessus correspond en fait exactement à celle utilisée par les chercheurs de l’université de Waterloo !
La seule différence est l’utilisation des fonctions min et max, qui permettent d’échanger potentiellement x1 et x2 pour s’assurer que C(x1)≥C(x2).
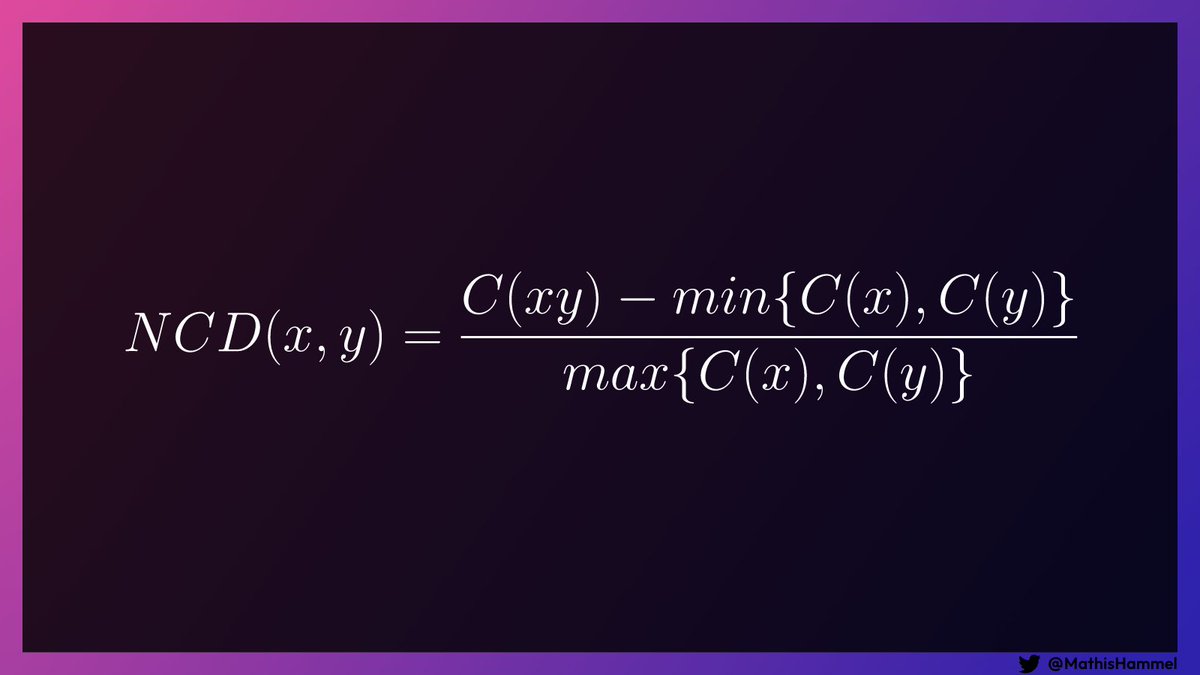
Avec cette formule, on peut maintenant créer un puissant classificateur : pour trouver la catégorie d’un texte x1 inconnu, on va chercher le texte x2 parmi le dataset d’entraînement qui s’en approche le plus.
Il est probable que la catégorie de x1 soit la même que x2.
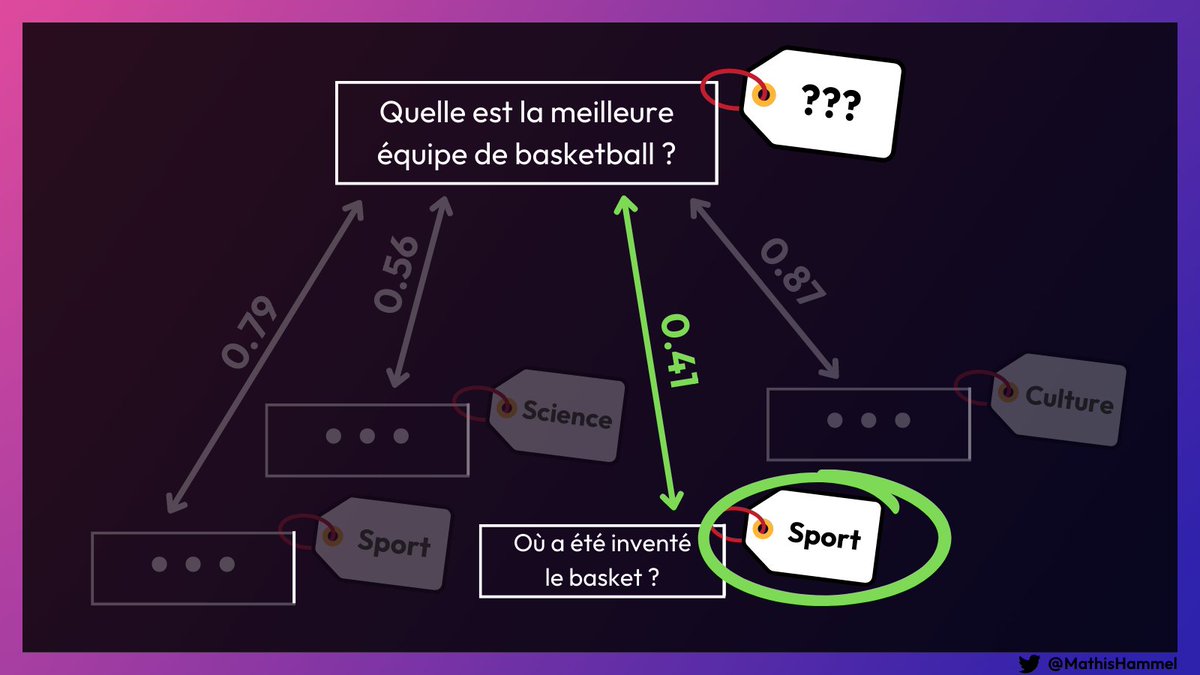
En pratique, les résultats sont impressionnants : sur un benchmark comprenant 13 modèles récents, cet algorithme parvient à se classer sur le podium à plusieurs reprises, et même en première place sur de nombreux datasets non-anglais !
Et même si BERT semble tout de même plus efficace que notre technique magique à base de gzip, cette dernière présente 3 avantages majeurs :
Avant de terminer cet article, je vous propose deux petites curiosités de code liées à ce papier.
La première est une erreur algorithmique que j’ai trouvée dans le code publié : un calcul pourrait être optimisé, voyez-vous lequel ? (indice : c’est dans les 3 dernières lignes)
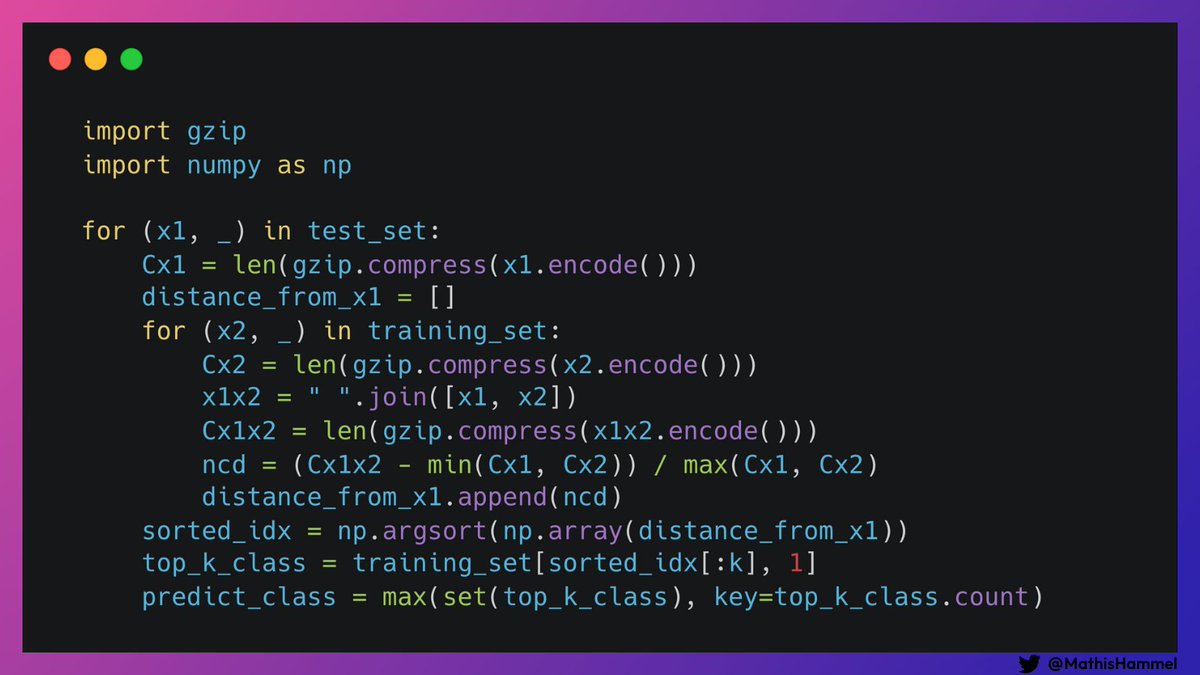
On peut constater ici que le code cherche les k textes les plus proches de chaque x1 dans le jeu d’entraînement, puis trouve la catégorie majoritaire parmi ceux-ci.
On appelle ça une recherche kNN (k Nearest Neighbors). Dans ce papier en particulier, les chercheurs prennent k=2.
Pour calculer les k plus proches voisins, l’implémentation du papier de recherche va faire quelque chose comme ça (via numpy.argsort) :

Cette opération est en réalité très inefficace : on appelle une fonction de tri sur un tableau gigantesque (jusqu’à 1,4 millions d’éléments pour le dataset Yahoo Answers), pour n’utiliser que les 2 premiers résultats…
En utilisant un tas binaire, structure de données spécialisée, on peut grandement améliorer la performance du calcul en ne gardant que les k meilleurs résultats au fil de l’exécution : la complexité temporelle de l’extraction passe de O(N·log(N)) à O(N·log(k)).

Et en pratique ?
Sur le dataset Yahoo Answers, on atteint un gain de performance de +16% grâce à mon optimisation, ce qui est loin d’être négligeable sur un benchmark qui demande 6 jours de calcul ! (La technique gzip est très lente car on doit calculer toutes les paires)
La seconde curiosité que je voulais vous montrer concerne la taille du code : c’est rare d’avoir un papier de recherche complet qui tient en 15 lignes de code, mais peut-on aller encore plus loin ?
En utilisant quelques techniques assez sales, j’ai réussi à faire passer le script de 538 à 214 caractères (en ajoutant au passage mon optimisation algorithmique 😇)
Je vous présente le meilleur classifieur de texte au monde qui tient en un tweet :
import gzip,heapq
g=lambda x:len(gzip.compress(x))
def classify(t):
A=g(t)
h=[(-1,)]*K
for(a,b)in train:heapq.heappushpop(h,((min(A,g(a))-g(t+b' '+a))/max(A,g(a)),b))
s=[x[1]for x in h]
return max(set(s),key=s.count)
C’est la fin de l’article, merci d’avoir tenu jusqu’au bout !
Il aurait pu être 2 fois plus court si je voulais aller droit au but, mais y’avait plein de petites digressions que je trouvais trop intéressantes. N’hésitez pas à partager ☺️
Et pour aller lire le papier de recherche complet, c’est par ici : https://aclanthology.org/2023.fi…
UPDATE : Il semble que les benchmarks de ce papier ont été un peu bidouillés pour gonfler le score du classificateur gzip. L’enquête de @_kenschutte est concordante avec les résultats que je calcule en local : https://kenschutte.com/gzip-knn-…
contact@mathishammel.com
Copier
contact@mathishammel.com