Qualifié en 24e place de la Meta Hacker Cup, voici mes solutions

Hier, je me suis classé 24e mondial sur la Meta Hacker Cup, une compétition de code réunissant plus de 27 000 participants !

Dans cet article, j’ai envie de vous expliquer comment j’ai résolu les 6 épreuves en moins de 2h. Vous allez voir, c’est pas si compliqué.

Commençons par un peu de contexte.

Facebook (désormais Meta) organise chaque année l’un des plus grands championnats de programmation au monde, qui leur sert notamment à repérer et recruter des développeurs·es d’élite.

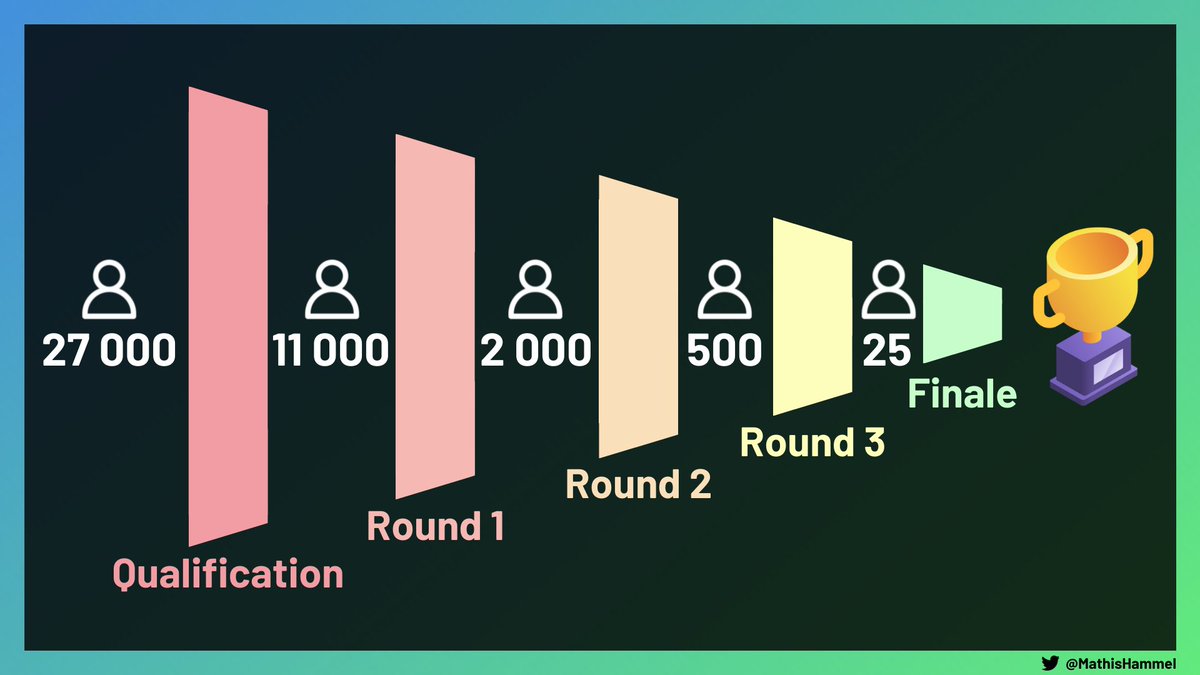
La Hacker Cup est organisée en 5 rounds de sélection.

Un problème d’algorithmique est quasiment toujours structuré de la même manière.

On nous donne un énoncé très précis du problème à résoudre, ainsi que des contraintes sur les grandeurs des données à traiter (par exemple “la liste comporte entre 1 et 1000 éléments”).

L’objectif est de coder un programme dans le langage de son choix (pour les compétitions j’adore Python) qui va prendre en entrée un jeu de données et produire en sortie la bonne réponse.

Notre code est ensuite testé sur des dizaines d’exemples pour vérifier qu’il est correct.

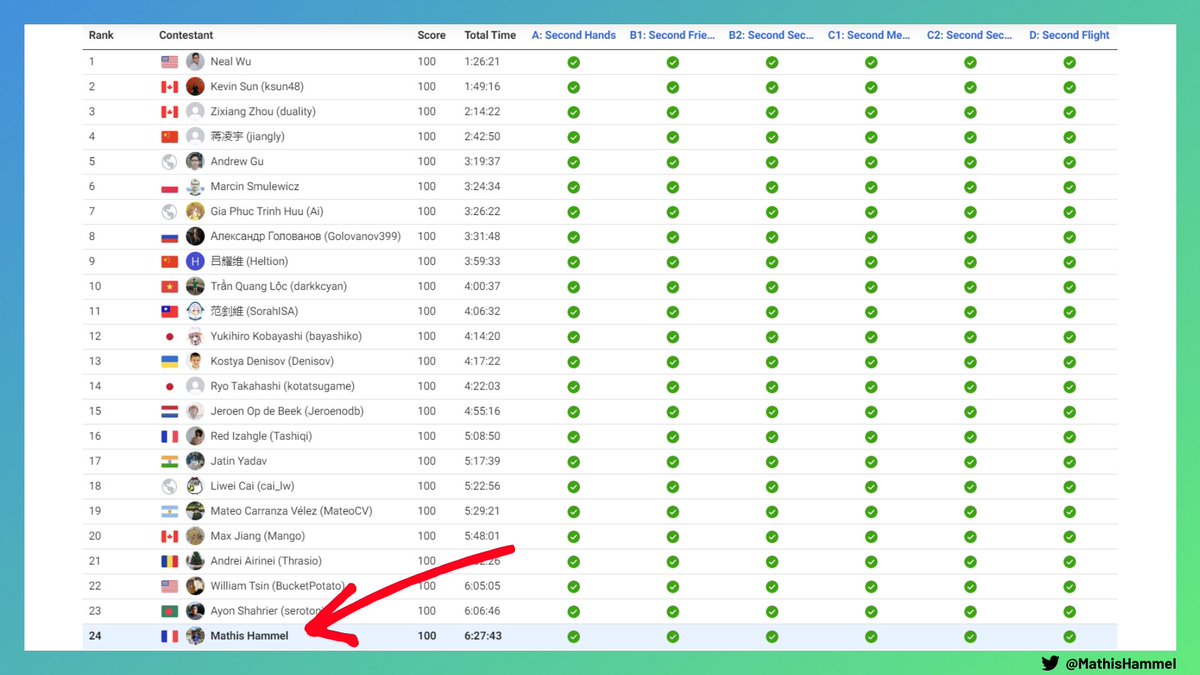
Le round de qualification de cette année comportait 6 épreuves, chacune rapportant un certain nombre de points.

Ici, les points n’avaient pas d’importance (il suffit de valider au moins un exo pour se qualifier) mais ils sont cruciaux pour le classement des rounds suivants.

Pour chacun des exercices, je vais vous expliquer mon anayse et ma manière de résoudre le problème. Pour commencer, le problème le plus facile de cette année, intitulé Second Hands.

On dispose de deux vitrines contenant chacune K socles, et on a N objets à afficher dans celles-ci.

Pour des raisons esthétiques, chaque vitrine ne peut pas contenir deux objets identiques.

On cherche à savoir s’il existe une configuration qui permet d’afficher tous les objets en vitrine et qui respecte cette contrainte.

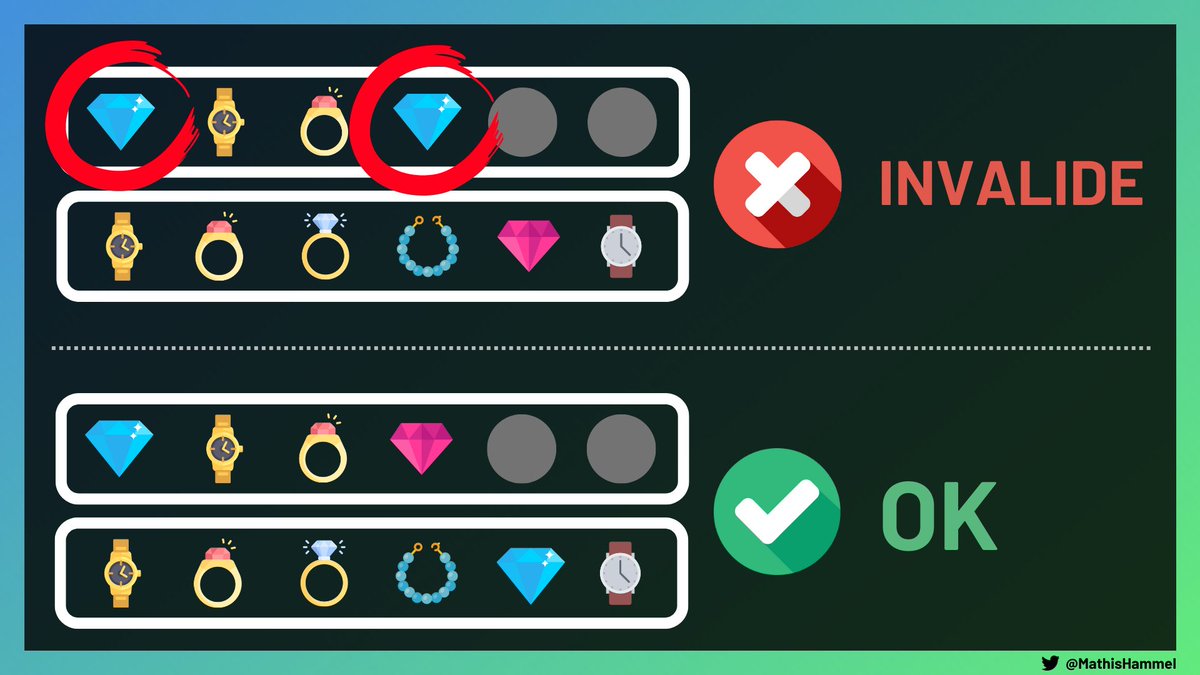
Pour commencer, on peut rapidement se rendre compte que s’il y a plus d’objets que de socles dans les vitrines (N > 2*K) alors on n’arrivera pas à tout faire rentrer.

Ça peut paraître évident, mais on peut facilement perdre des points en oubliant de vérifier cette condition !

L’autre vérification à effectuer concerne les différents types d’objets :

• Si un objet est présent en un seul exemplaire, il peut aller dans n’importe quelle vitrine.
• Avec deux exemplaires, on doit en mettre un dans chaque vitrine.
• Au-delà de 3, c’est impossible.

Si on a suffisamment de place dans les vitrines (condition 1) et que les groupes d’objets identiques n’ont jamais plus de 2 exemplaires (condition 2), alors il existe forcément un agencement des objets qui fonctionnera.

Cet exo se résout donc en quelques lignes :

Pour l’exercice B intitulé “Second Friend”, on va devoir planter des arbres. Cet exercice est séparé en deux sous-problèmes (B1 et B2) de difficulté croissante que l’on peut résoudre indépendamment.

Le principe du sous-problème B1 est simple : on a des arbres plantés sur une grille de forme rectangulaire.

Notre objectif est d’en planter d’autres pour que chaque arbre de la grille finale ait au moins deux voisins (diagonales exclues) :

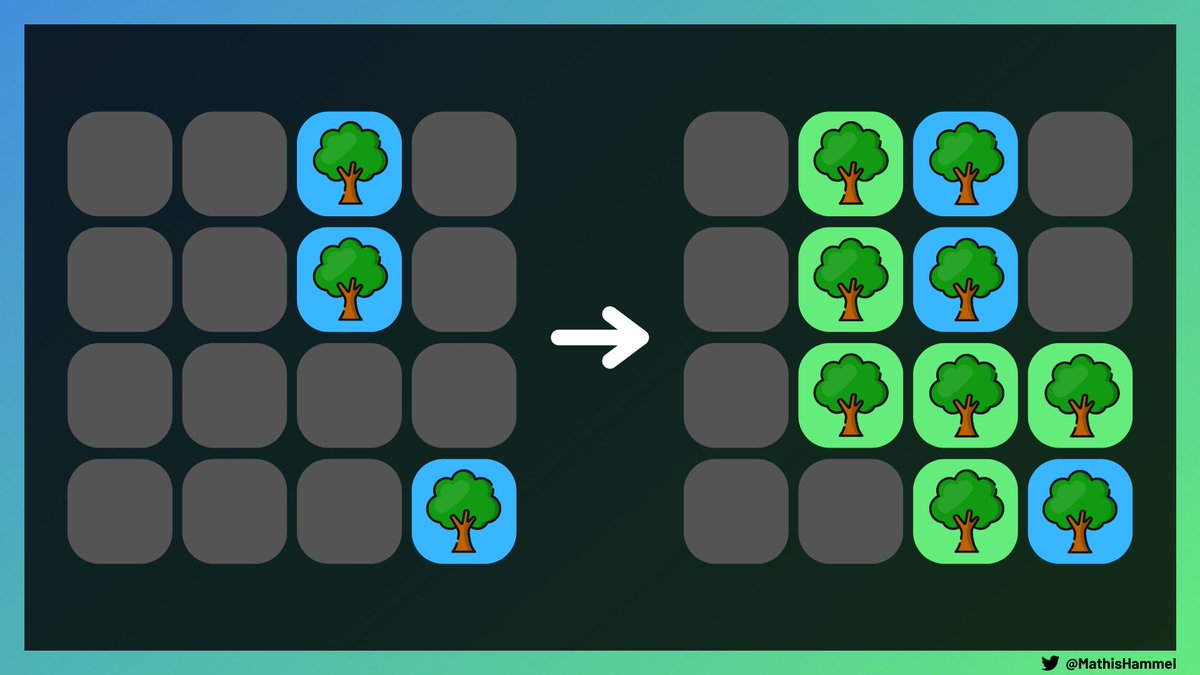
Ici, on a de la chance sur l’énoncé : il est demandé de renvoyer n’importe quelle solution valide, sans contrainte sur le nombre d’arbres plantés.

Du coup, il existe une solution assez évidente : on plante des arbres PARTOUT.

En effet, chaque arbre aura un nombre satisfaisant de voisins avec cette solution :

• Les coins ont 2 voisins
• Les bords en ont 3
• Tous les autres en ont 4

Mais en fait, cette solution ne marche pas toujours.

Est-ce que vous arrivez à trouver un cas particulier qui peut servir de contre-exemple ?

Effectivement, si la grille est trop petite alors ça va coincer : certaines cellules n’auront qu’un seul voisin !

Il faut donc bien prêter attention aux contraintes fournies dans l’énoncé, qui indiquaient que la largeur et la hauteur minimale de la grille étaient de 1.

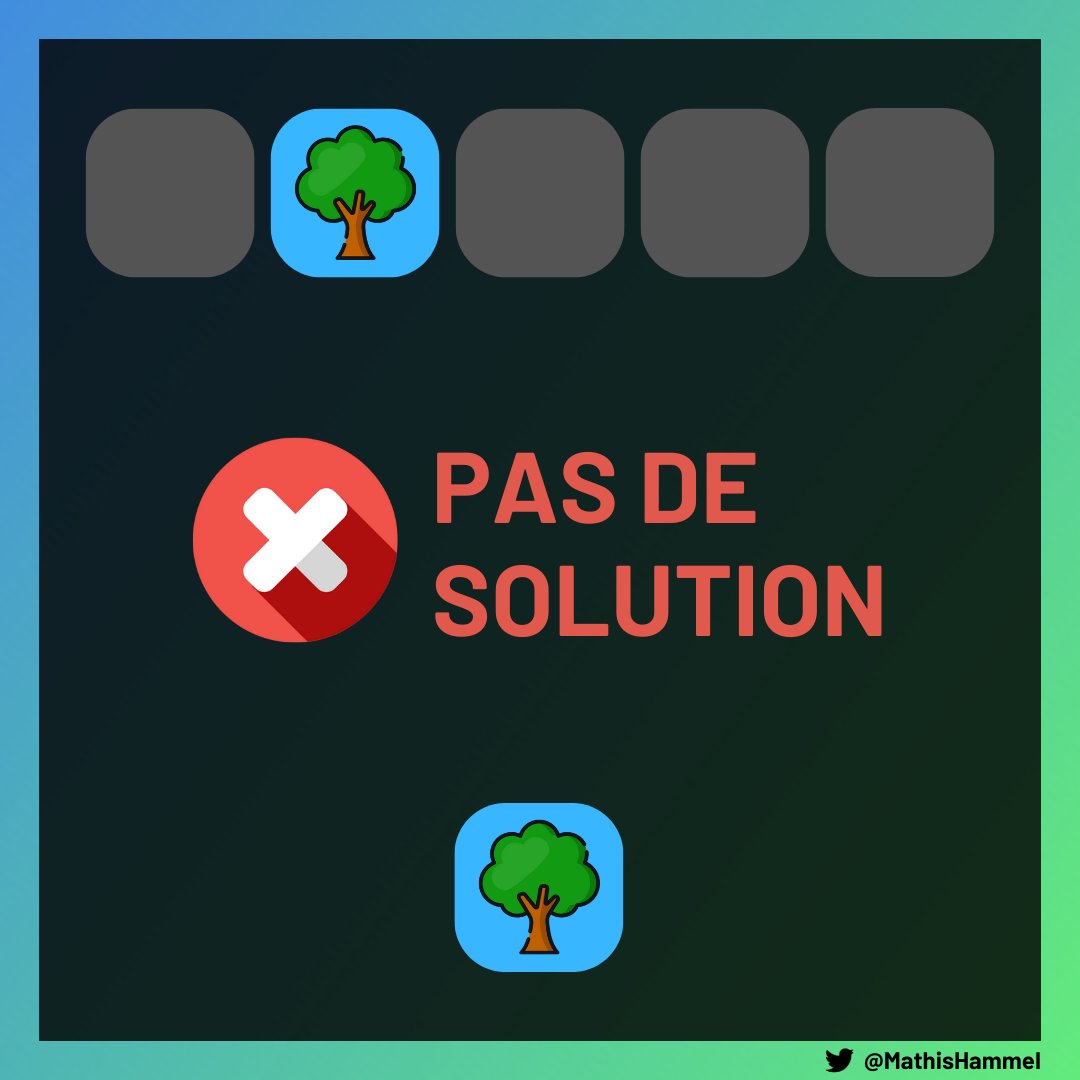
Et on a d’ailleurs un contre-exemple dans ce contre-exemple !

Si la grille a une largeur et/ou hauteur égale à 1 mais qu’aucun arbre n’est présent initialement, il suffit de n’en planter aucun ;)

En tout, ça nous fait donc trois cas possibles à vérifier :

1. Si aucun arbre présent initialement : la solution est un champ vide
2. Si la largeur ou la hauteur sont égales à 1 : pas de solution
3. Dans tous les autres cas, la solution est un champ entièrement rempli d’arbres

Passons maintenant à l’exercice B2, qui est la suite du précédent.

Le principe est ici le même, en ajoutant un élément perturbateur : des pierres sont présentes sur la grille et nous empêchent de planter des arbres sur certains emplacements.

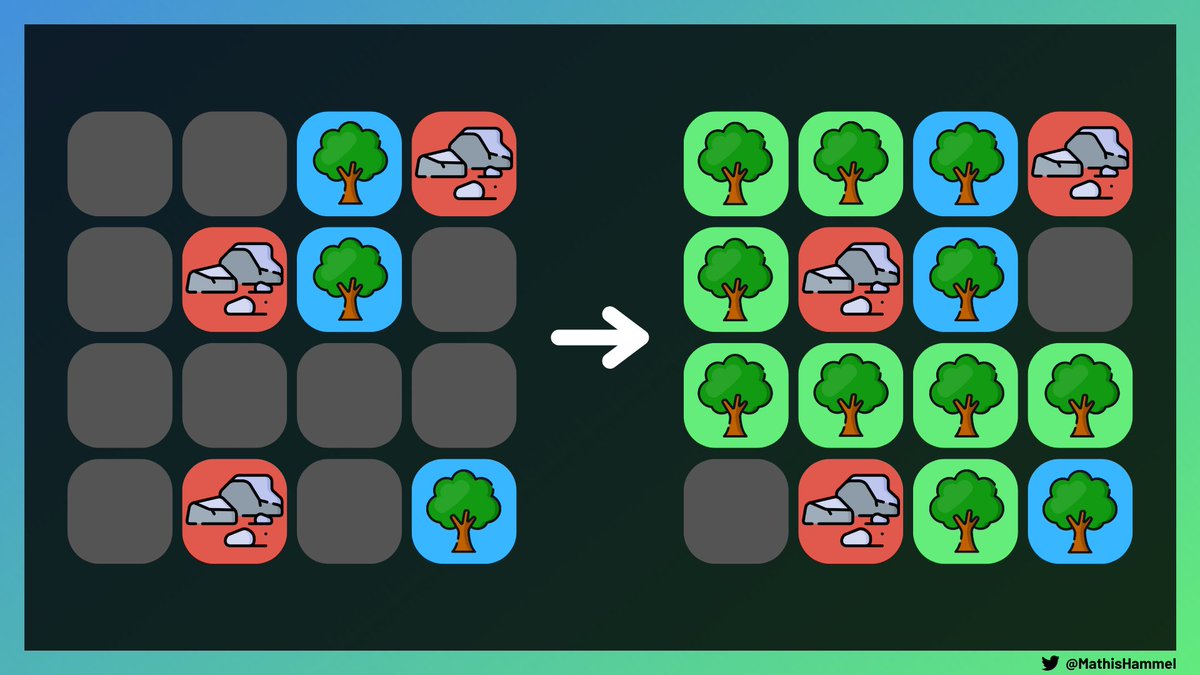
Pour résoudre ce challenge, il va falloir créer un algorithme plus intelligent que pour le sous-problème B1.

En effet, placer un arbre dans chaque emplacement disponible risque de créer des solutions invalides :

Ce qui pose problème, ce sont les pierres qui vont créer des impasses étroites dans lesquelles aucun arbre ne pourra être présent.

Dans cet exemple, on peut créer un premier “chemin” d’arbres valide sur les cases marquées d’un point jaune, qui ont chacune au moins deux voisins.

Mais pour ajouter un second voisin à notre arbre placé initialement, il va aussi falloir en ajouter successivement sur ce chemin, qui se termine par un cul-de-sac ayant un seul voisin possible.

Cette configuration initiale n’admet donc pas de solution.

Ce qu’il faut donc remarquer pour résoudre ce problème, c’est que certains emplacements sont interdits : c’est là où il n’existe qu’un seul voisin potentiel.

En marquant ces cases interdites, on se rend compte que ça crée de nouveaux emplacements n’ayant à leur tour qu’un seul voisin potentiel :

On peut ainsi propager cet ensemble pour déterminer tous les emplacements sur lesquels aucune solution valide ne comportera d’arbres.

À la fin de ce processus, toutes les cases n’ayant pas été marquées comptent au moins deux voisins et on peut placer un arbre dessus !

Si un arbre était initialement placé sur une cellule interdite, alors aucune solution n’existe.

Sinon, il suffit de planter un arbre sur chaque emplacement non marqué et ça nous donne une configuration valide 🙂

Pour résoudre ce problème de propagation efficacement, on peut utiliser un algorithme de recherche en largeur, souvent appelé BFS (pour “Breadth-First Search”).

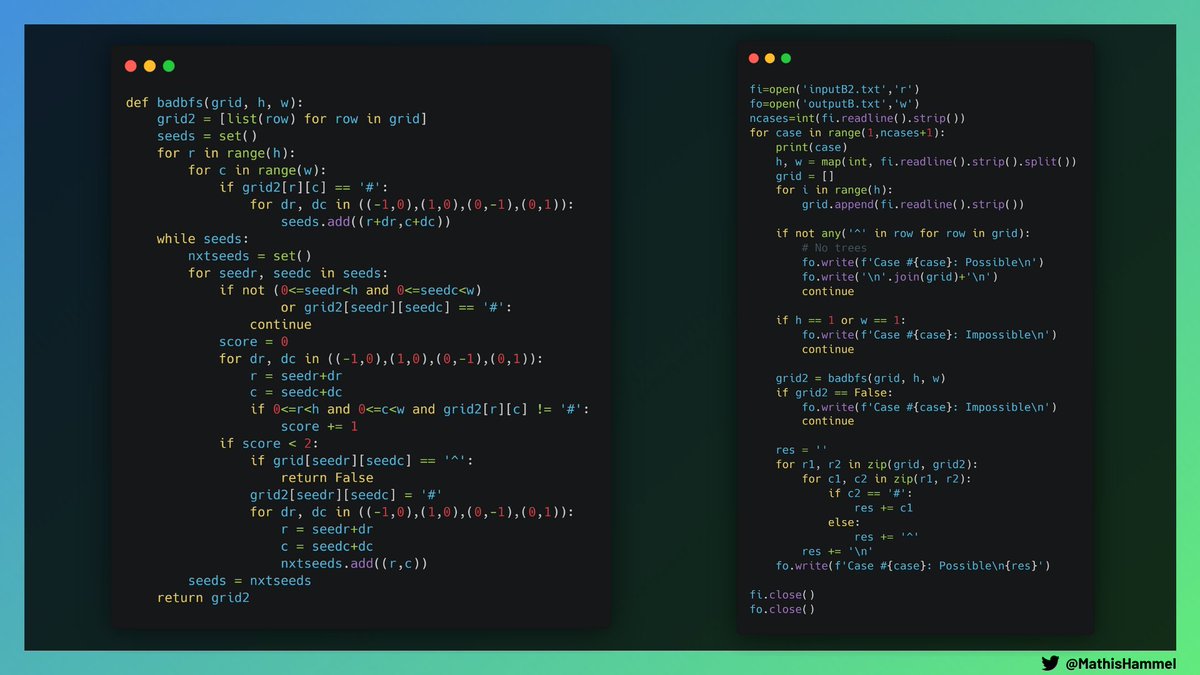
Je vous épargne les détails d’implémentation, mais vous pouvez lire ci-dessous ma solution telle que je l’ai codée pendant l’épreuve, sans retouche (attention, code très sale).

D’après les logs, j’ai mis 29 minutes entre l’ouverture de l’énoncé et la dernière ligne de code !

Passons à l’exercice C, que j’ai étonnamment trouvé plus facile que le B alors qu’il rapportait plus de points. C’est parti pour “Second Meaning” !

(Oui, tous les titres d’exos commencent par “Second”, c’était le thème de ce round)

Ce problème est basé sur l’ambiguïté du décodage en morse si on retire les espaces. Prenons par exemple la chaîne •–••-•-•• :

• En l’interprétant comme • --• •- •-••, on obtient le mot EGAL
• En l’interprétant comme •-- •• -• -••, on obtient le mot WIND

Dans cet exercice, il faut créer un nouvel alphabet morse, de telle sorte qu’il n’existe aucune chaîne de points et de tirets qui admette plusieurs décodages possibles.

Le premier symbole de cet alphabet nous est imposé, et il faut inventer les autres.

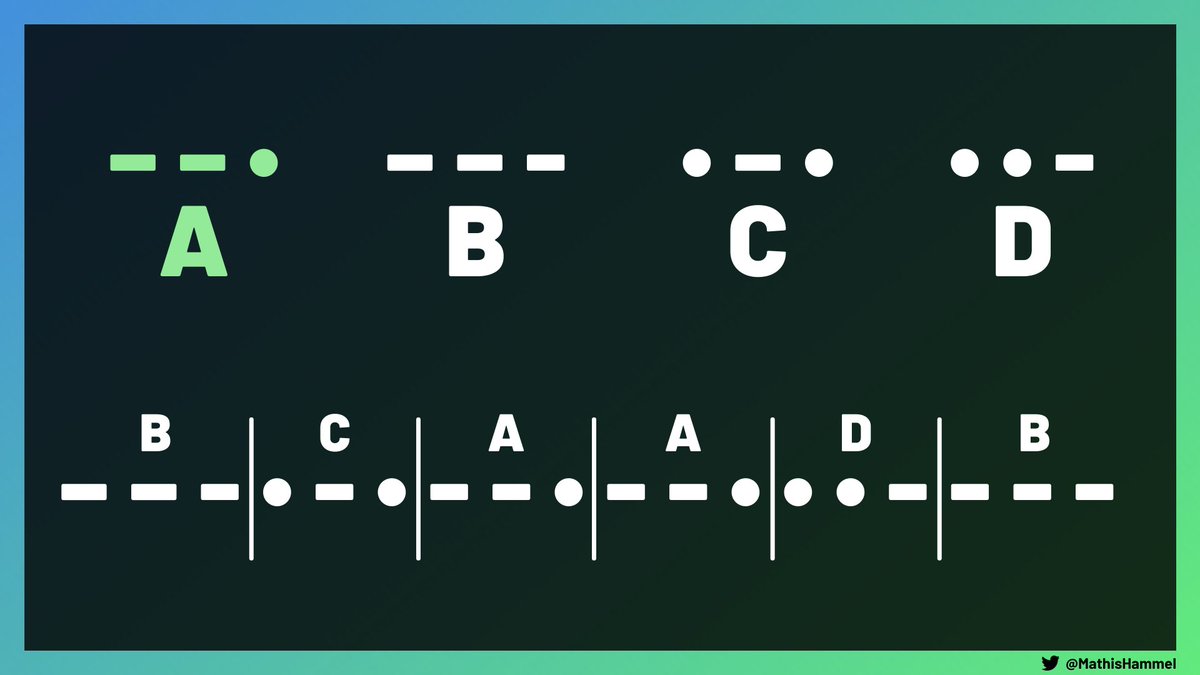
Par exemple, si on nous demande un alphabet de 4 lettres avec le symbole –• imposé, on peut proposer l’alphabet ci-dessous.

Comme tous les symboles font 3 caractères, le décodage d’une chaîne consiste à décoder chaque bloc de 3 caractères successivement.

Prenons maintenant un cas plus difficile : on nous demande un autre alphabet de 4 lettres, cette fois-ci avec • comme premier symbole.

Pas possible cette fois de créer 4 lettres différentes ayant toutes la même longueur, mais on peut quand même trouver une solution.

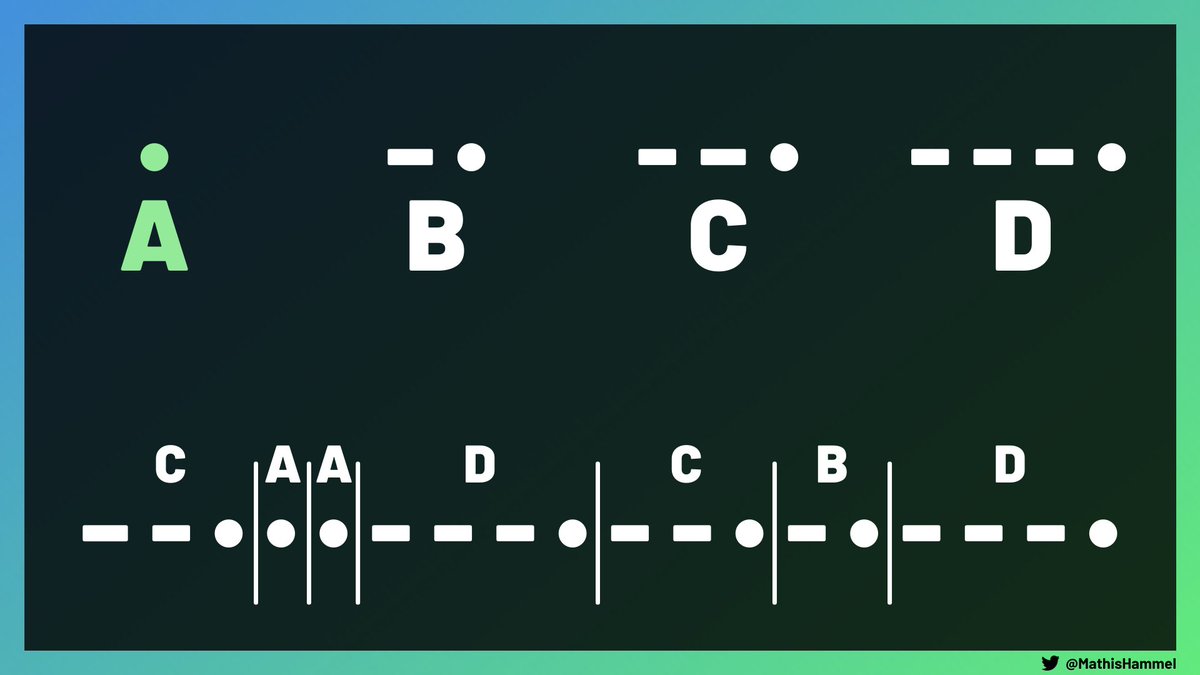
Un alphabet qui respecte la propriété demandée est appelé “code préfixe” : aucun de ses symboles n’est le préfixe d’un autre.

Ainsi, le symbole ••-• peut cohabiter avec ••– et - dans un alphabet, mais pas avec •• ni ••-•–

Les formes les plus connues de code préfixe sont la compression de Huffman et les caractères UTF-8, et c’est aussi le cas des indicatifs téléphoniques internationaux !

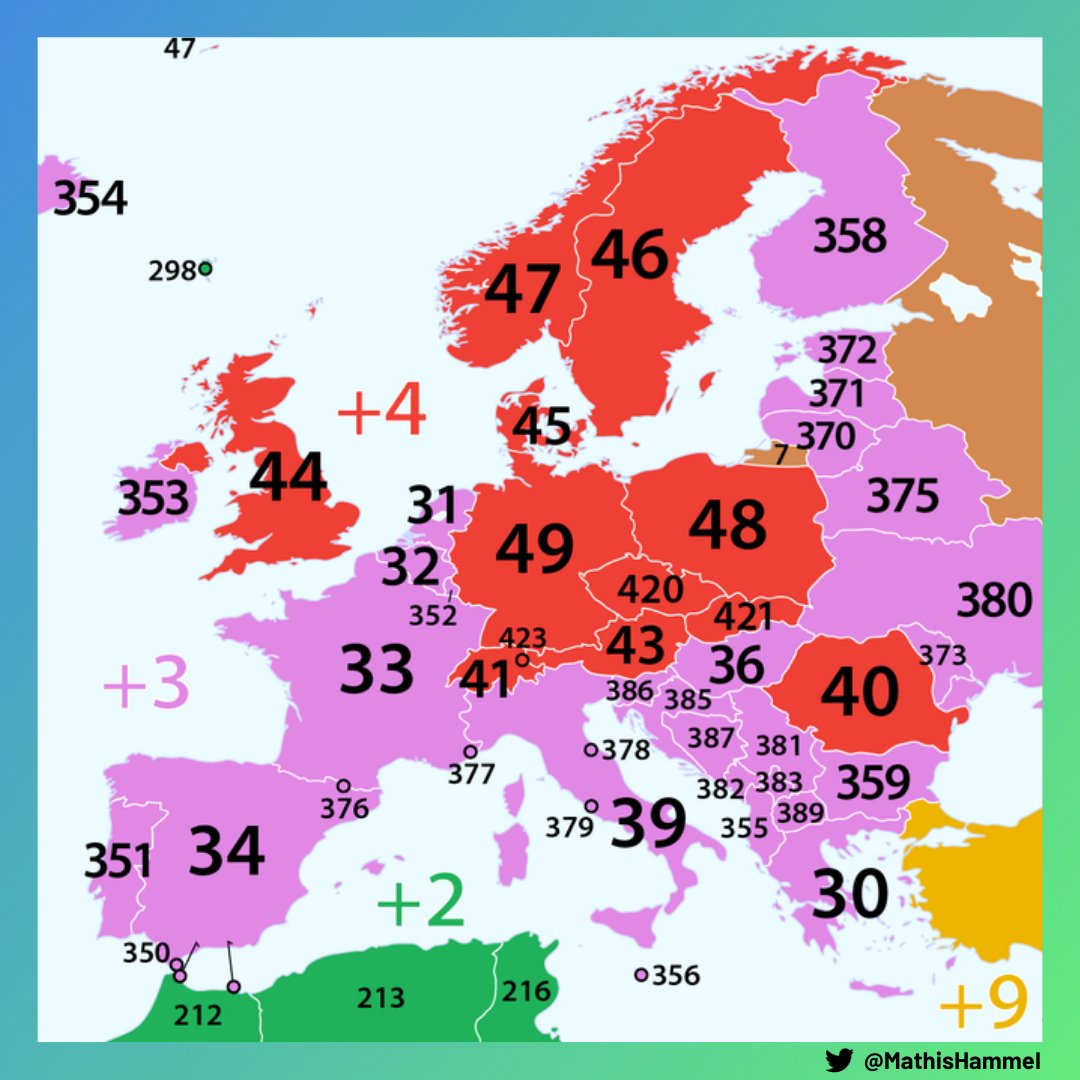
Les contraintes de l’énoncé nous disent que la taille demandée pour l’alphabet est comprise entre 2 et 100. Chaque symbole peut contenir entre 1 et 200 caractères.

Le sous-problème C2 est identique, à l’exception de ce nombre maximal de caractères par symbole qui est de 10.

La première solution que j’ai trouvée permet de résoudre directement les deux sous-problèmes, ce qui m’a permis de gagner un peu de temps.

On va créer un alphabet où toutes les lettres (sauf la première qu’on ne choisit pas) vont faire exactement 10 caractères de long.

Il existe 2^10 = 1024 symboles en morse de longueur 10. Aucun n’est le préfixe d’un autre comme ils sont distincts et font la même longueur, donc on peut générer un code préfixe composé de 1024 symboles.

Le premier code de l’alphabet nous est imposé, mais ça ne pose pas vraiment de problème : il suffit d’éliminer de notre code tous les symboles incompatibles.

Dans le pire cas, le symbole imposé contient un seul caractère (• ou -), et élimine la moitié des symboles de notre alphabet potentiel.

Mais les 512 qui nous restent suffisent largement comme la taille maximale de l’alphabet demandé est de 100.

Et voici le code de ma solution, avec itertools qui nous permet de générer tous les symboles en une ligne au lieu de s’embêter avec 10 boucles imbriquées ou des bitmasks.

Le dernier problème, intitulé “Second Flight” était le plus difficile de cette épreuve de qualification. Il s’agissait de calculer des capacités de flux de voyageurs entre deux destinations sur un réseau aérien.

On a plusieurs aéroports reliés par des lignes aériennes. Chaque ligne est desservie deux fois par jour (matin et soir) dans les deux sens, par des avions de capacité donnée.

Il faut calculer le nombre maximal de passagers par jour pouvant aller entre deux destinations données.

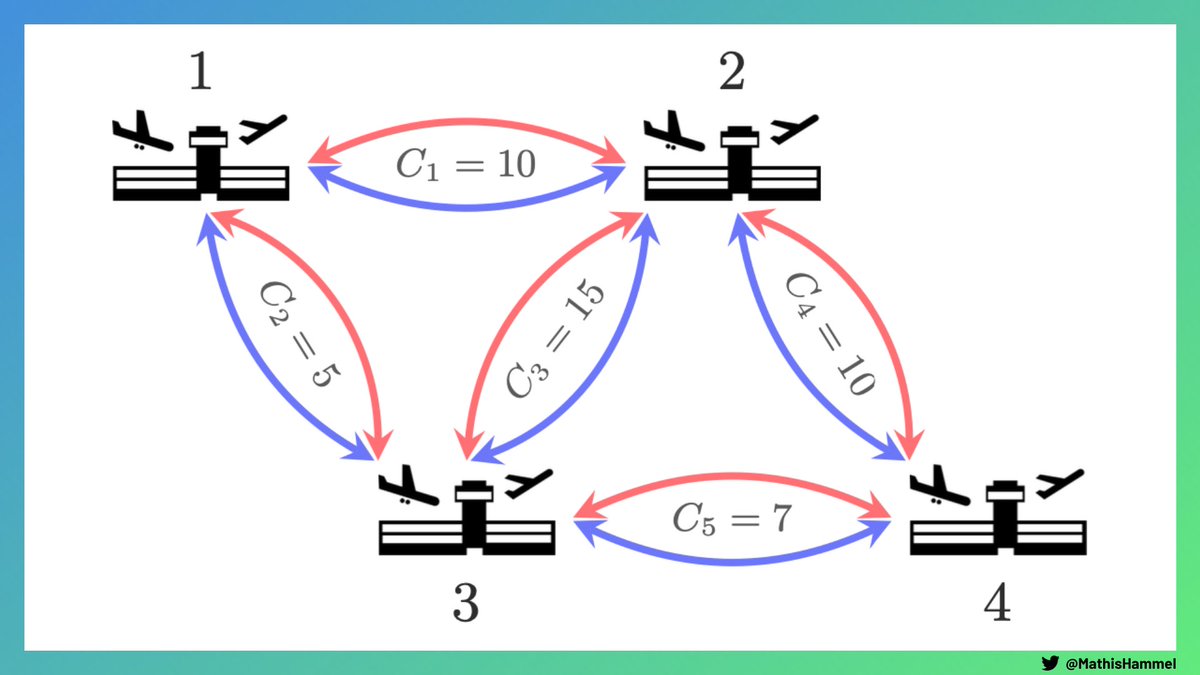
Les algorithmiciens auront déjà reconnu une variante du problème de flot maximal dans un DAG et dégainé l’artillerie lourde avec l’algorithme d’Edmonds-Karp ou de Dinic.

En fait, cette solution est incorrecte car trop lente, et il existe plus simple.

L’énoncé nous dit qu’on peut avoir jusqu’à 200 000 aéroports et 200 000 lignes aériennes dans notre réseau aérien.

En plus de ça, on doit pouvoir traiter jusqu’à 200 000 calculs de capacités entre différentes paires d’aéroports. On va donc devoir bien optimiser l’algo.

Pour aller d’une ville A vers une autre ville B, un passager a trois options :

• Prendre le vol A->B du matin
• Prendre le vol A->B du soir
• Faire escale dans une tierce ville X : prendre le vol A->X le matin et X->B le soir

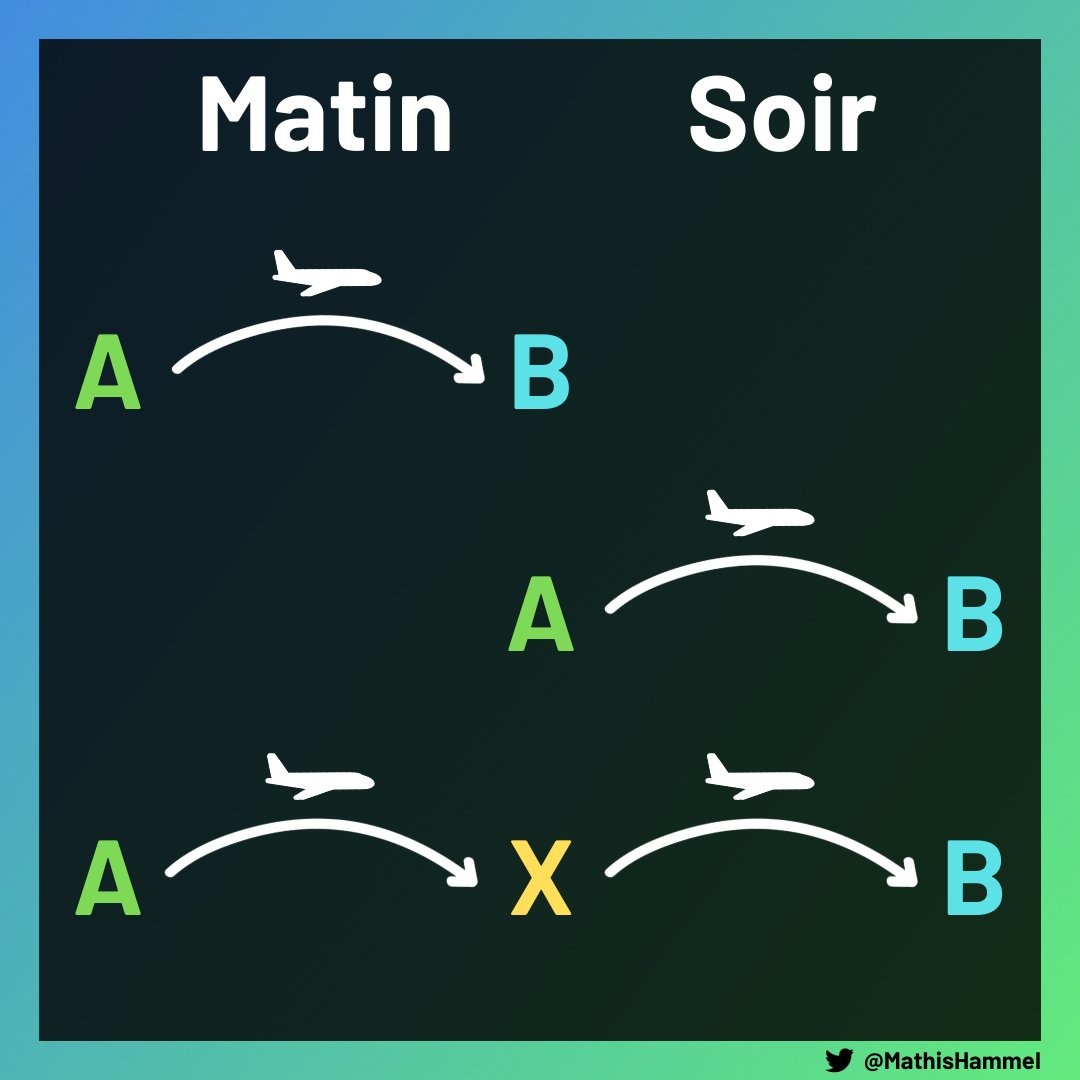
Pour connaître la capacité maximale journalière entre deux villes, il faut donc compter deux fois la capacité du trajet A->B, puis la capacité de chaque trajet avec escale (égale à la plus petite capacité des deux vols qui la composent).

La complexité de cette fonction est O(N) car on parcourt l’ensemble des villes dans une boucle.

En multipliant ça par 200 000 requêtes, on se rend compte qu’il faudrait plusieurs minutes pour traiter chaque jeu de test, ce qui est trop lent.

Voyons comment améliorer ça.

La première optimisation consiste à ne pas parcourir toutes les villes, mais seulement besoin de celles qui sont reliées à A et à B : les autres ont de toute façon une capacité de 0.

Trouver les villes en question revient à faire un calcul d’intersection entre deux ensembles.

Pour ce calcul, on regarde laquelle ville a le moins de lignes aériennes, et on itère sur celles-ci.

La complexité du calcul est O(min(nA, nB)), avec nA et nB le nombre de villes reliées à A et B respectivement.

Alors c’est vrai, il est possible que A et B soient chacune reliées à un très grand nombre de villes, auquel cas l’optimisation précédente ne permet pas d’accélérer le calcul.

Cependant, l’énoncé nous indique qu’il n’y a pas plus de 200 000 lignes aériennes en tout.

Sachant qu’entre 200 000 aéroports il existe plus de 19 milliards de lignes aériennes possibles, la limitation du nombre effectif de lignes utilisées nous permet de découvrir une propriété intéressante du graphe.

Intuitivement, on peut voir que même si certaines paires peuvent avoir un calcul assez lent (car A et B sont toutes les deux reliées à un grand nombre de villes), ces paires sont forcément en nombre limité.

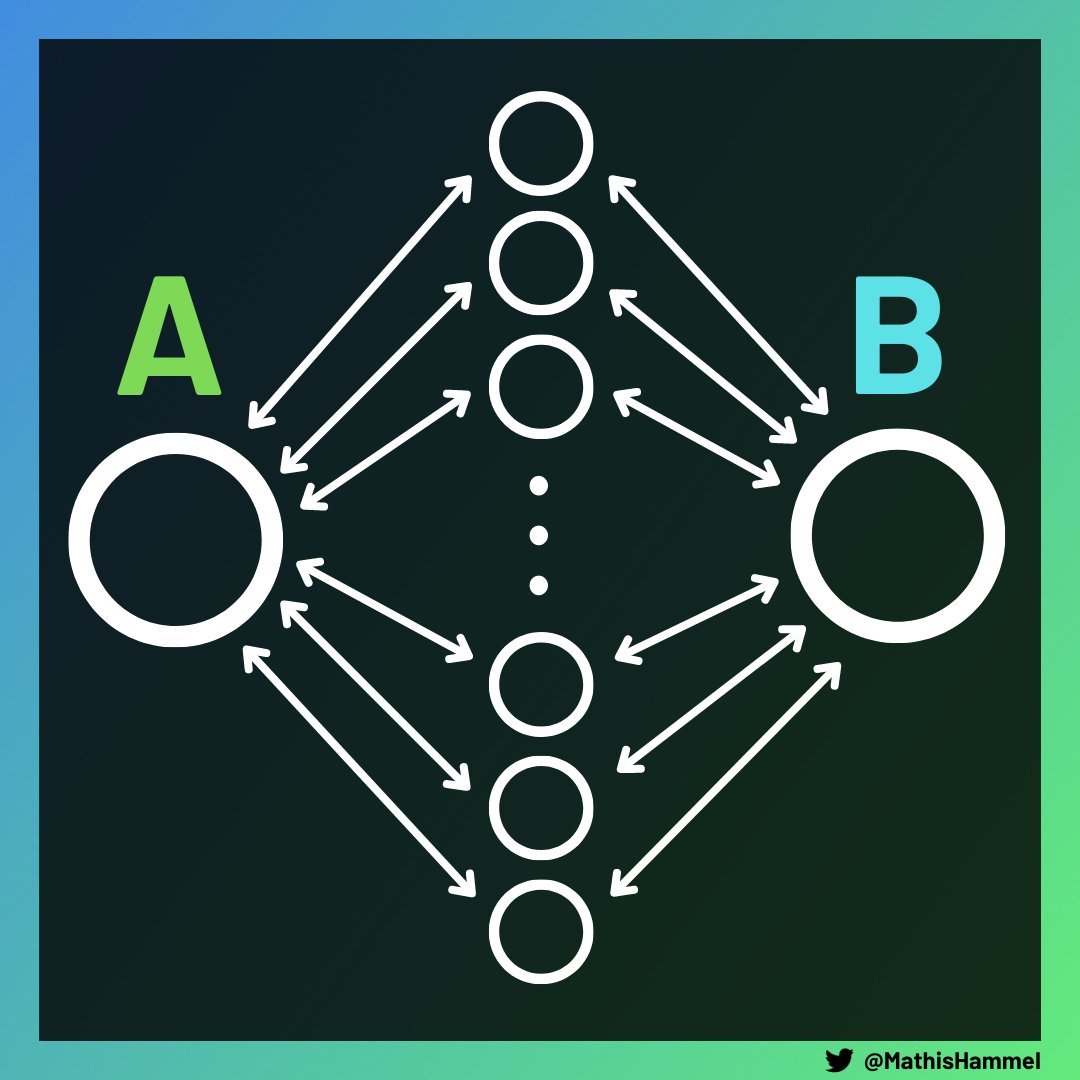
Si A et B sont chacune reliées à 100 000 villes, alors toutes les lignes aériennes sont allouées et chaque autre ville n’est reliée qu’à A et B. Le calcul de n’importe quelle autre paire sera donc quasi instantané grâce à la complexité O(min(nA, nB)) établie plus tôt.

Il reste un piège : même s’il existe un faible nombre de requêtes “lentes” possibles, qu’est-ce qui les empêche de nous faire calculer plein de fois la même route lente ? En réalité, ce n’est pas un problème.

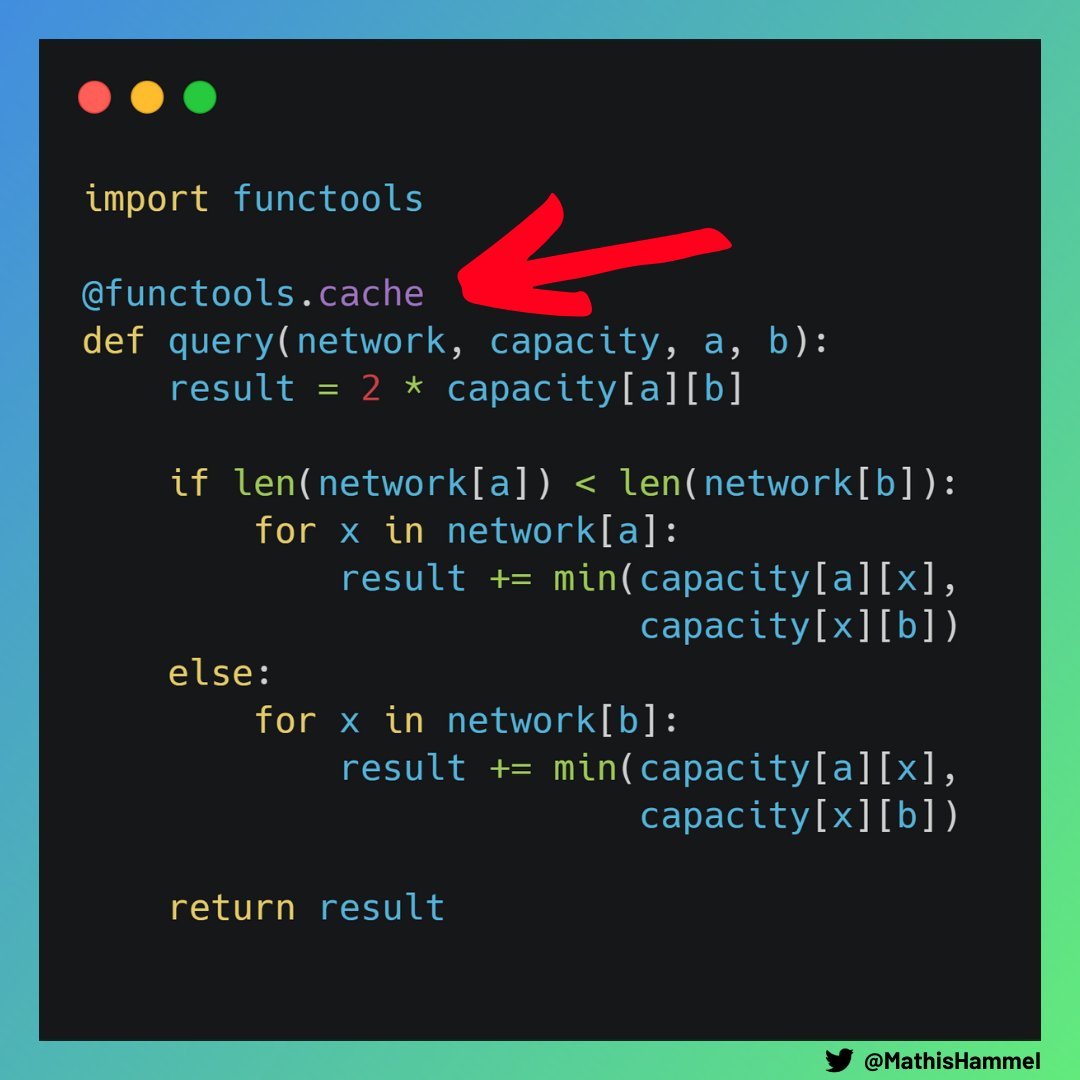
Comme une même requête aura toujours le même résultat, il nous suffit de sauvegarder tous les résultats précédents.

Ainsi, on n’aura pas à refaire le calcul au cas où une demande soit répétée plusieurs fois. Ça s’appelle la mémoïsation, et c’est trivial à implémenter en Python !

Cet article est terminé, j’espère que ce corrigé vous a plu 😄

L’explication du dernier problème est bien touffue malgré la solution simple en apparence, bravo d’avoir tenu jusqu’au bout !

Si vous voulez continuer à améliorer votre niveau en algo, je poste chaque semaine un petit challenge et sa correction pour s’entraîner aux entretiens d’embauche, que vous retrouverez dans cet article.

Si vous avez l’oeil, vous aurez peut-être remarqué que plusieurs images de cet article ont été générées par l’intelligence artificielle Midjourney.

Pour comprendre comment ces modèles fonctionnent, retrouvez les explications techniques dans mon dernier article !