404CTF 2024 - Sea side channel

Ce challenge en 4 parties est l’un de ceux qui a été le moins flaggé sur le 404CTF, avec seulement 2 personnes qui l’ont validé en entier.

Malgré une apparence ultra technique et très mathématique, je pense que ce challenge était finalement plus simple qu’il n’en avait l’air, surtout pour la partie 1/4 qui pouvait se contourner entièrement.

L’épreuve est basée sur le cryptosystème CSIDH (prononcé “sea side”, d’où le nom du challenge), qui est un protocole d’échange de clés dérivé du très célèbre Diffie-Hellman. Le jour où quelqu’un mettra au point un ordinateur quantique de puissance raisonnable, il sera en mesure de casser Diffie-Hellman, et donc compromettre la sécurité de 99% des communications chiffrées sur internet. Pour répondre à ce problème, les chercheurs en cryptographie font la course depuis plusieurs années pour trouver des algorithmes de chiffrement qui seraient capables de résister à un tel ordinateur : on appelle ça la cryptographie post-quantique, et CSIDH fait partie de ces algorithmes candidats.

Partie 1/4

Le principe du premier challenge est d’implémenter notre propre version de CSIDH.

Pour cela, on nous donne un notebook Sage qui nous présente le fonctionnement du protocole, et nous affiche le flag si on a correctement implémenté toutes les fonctions utilisées.

Ce writeup ne détaillera pas le fonctionnement de CSIDH en profondeur, vous verrez que certaines de ses notions ne sont pas obligatoires pour valider les 4 parties. Cependant, il faut savoir que c’est un protocole d’échange de clés basé sur Diffie-Hellman : il permet à deux personnes de générer séparément une même valeur secrète, sans qu’il ne soit possible de reconstituer cette valeur en espionnant leurs échanges.

J’aime beaucoup l’illustration de Wikipédia pour illustrer Diffie-Hellman, qui présente une très bonne analogie avec des peintures de couleur :

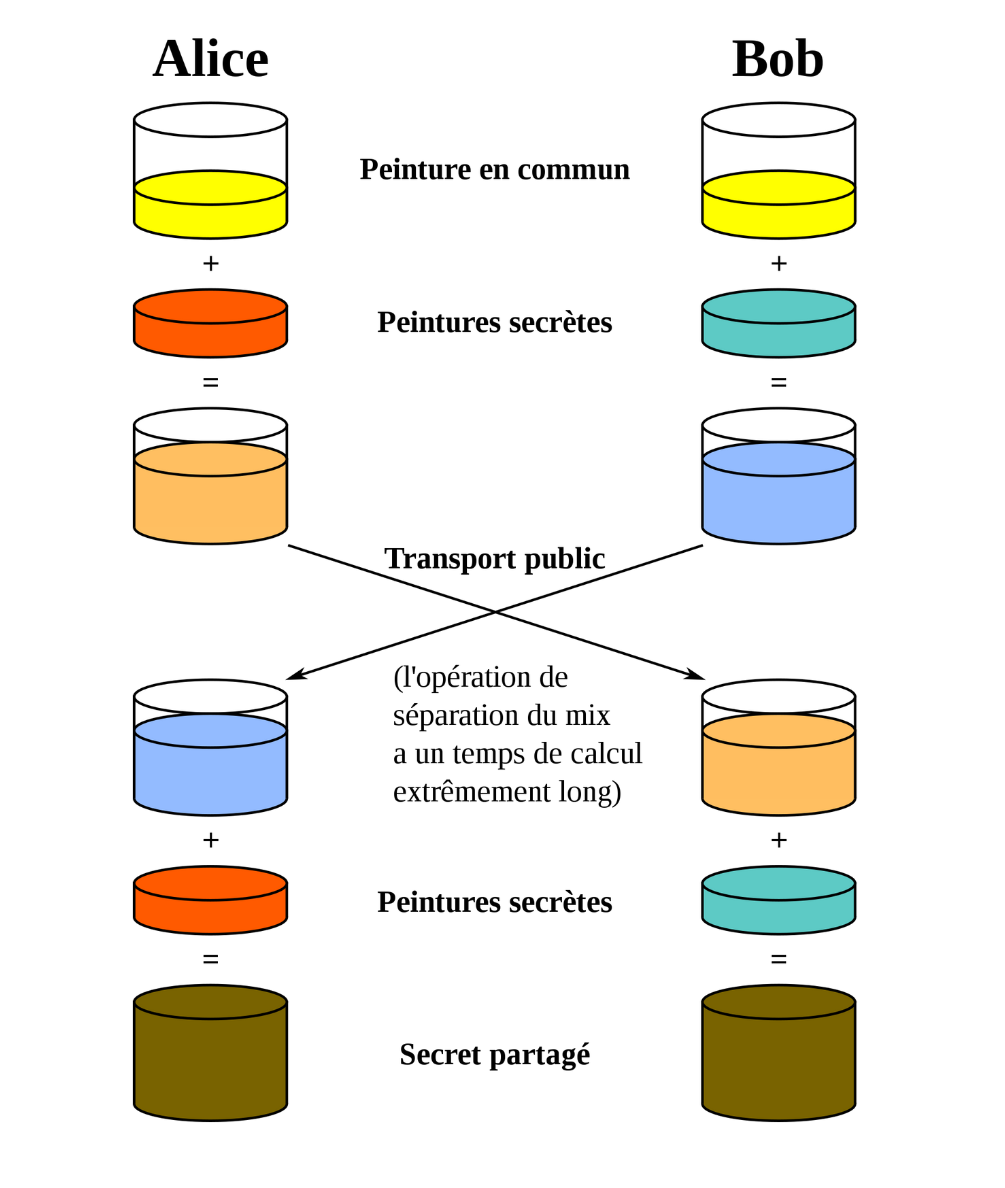
Dans le cas de Diffie-Hellman classique, les peintures sont en réalité des nombres, et le mélange se fait avec des multiplications. Pour CSIDH, on utilise des objets mathématiques légèrement plus complexes : il s’agit de courbes elliptiques supersingulières sur des corps finis d’ordre premier. À méditer.

Pour valider le premier challenge, on doit procéder à un échange de clés CSIDH : à partir de la valeur publique d’Alice et la valeur secrète de Bob, il faut reconstituer le secret partagé. Ce secret partagé est un nombre, qui sera ensuite transformé en clé AES pour déchiffrer le flag :

Shared_secret = evaluate_class_group_action_positive(......).a2() # TODO

# La clé AES est composée des 16 premiers bytes du MD5 du Shared_secret
hash = MD5.new(long_to_bytes(int(Shared_secret)))
key=hash.digest()[:16]

# On déchiffre le flag avec la clé AES obtenue
cipher = AES.new(key, AES.MODE_ECB)
decrypted_message = cipher.decrypt(b'\xe67\x98\xc7\xccU5\xf5\xd2\xfd\xd4...')
unpadded_message = unpad(decrypted_message, AES.block_size)
print(unpadded_message.decode())

Pour cette série de challenges, on nous fait travailler sur une version minimaliste de CSIDH définie sur un un corps fini d’ordre 419 : en d’autres termes, tous les nombres utilisés sont des entiers compris entre 0 et 418.

La valeur Shared_secret ne fait pas exception, et on va donc pouvoir très simplement la bruteforcer :

for Shared_secret in range(419):
    hash = MD5.new(long_to_bytes(int(Shared_secret)))
    key=hash.digest()[:16]

    try:
        cipher = AES.new(key, AES.MODE_ECB)
        decrypted_message = cipher.decrypt(b'\xe67\x98\xc7\xccU5\xf5\xd2\xfd\xd4...')
        unpadded_message = unpad(decrypted_message, AES.block_size)
        print(unpadded_message.decode())
    except ValueError:
        # Padding incorrect = mauvaise clé, on ignore
        pass

Sans même avoir codé la moindre fonction de CSIDH, on peut complètement contourner le challenge et récupérer le flag :

"Personne ne pourra nous écouter ! 404CTF{C4lcul_d'1s0g3n135_3n_b0rd_d3_m3r}"

Partie 2/4

Pour les parties 2, 3 et 4, on travaille sur une implémentation Rust de CSIDH qui nous est fournie, on n’a donc pas besoin d’utiliser la partie 1.

Ces trois parties utilisent le même principe : on veut connaître la clé privée de Bob en analysant la consommation électrique de son processeur. En effet, certaines opérations mathématiques sont plus intenses à calculer que d’autres, et une capture très précise peut nous permettre de distinguer les différentes phases de l’algorithme et retrouver certaines propriétés de sa clé privée.

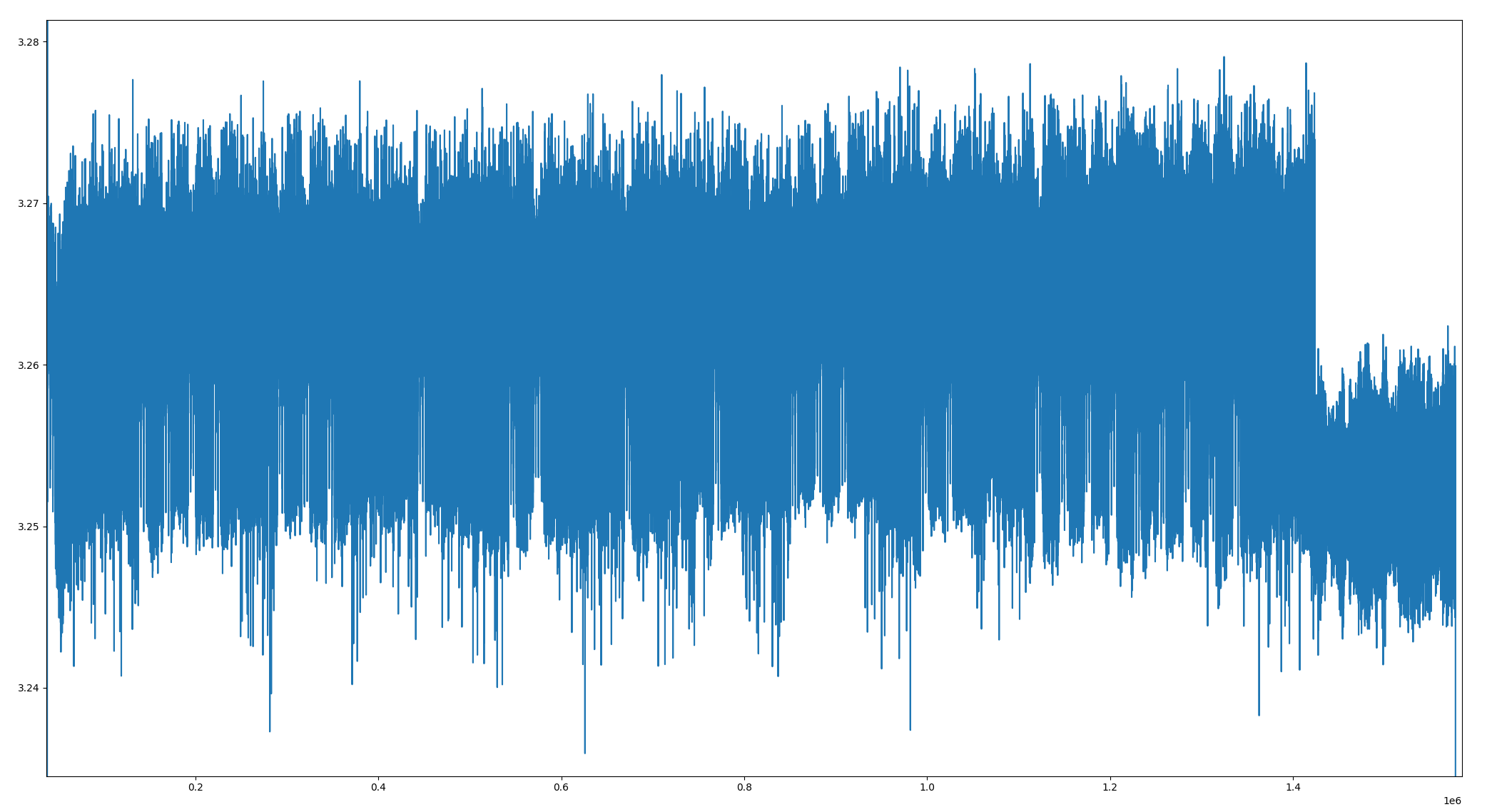
Cette capture est effectuée par un oscilloscope réglé pour enregistrer la tension du processeur plusieurs millions de fois par seconde, avec une précision de l’ordre du microvolt.

Même si on voit aperçoit quelques motifs intéressants apparaître sur la capture ci-dessus, celle-ci semble quand même très indigeste. Heureusement, le créateur du chall nous donne un joker très solide pour cette épreuve : les triggers.

En plus de la capture principale, on nous donne ces 3 signaux auxiliaires (T1, T2 et T3) qui décrivent l’étape de l’algorithme en cours d’exécution.

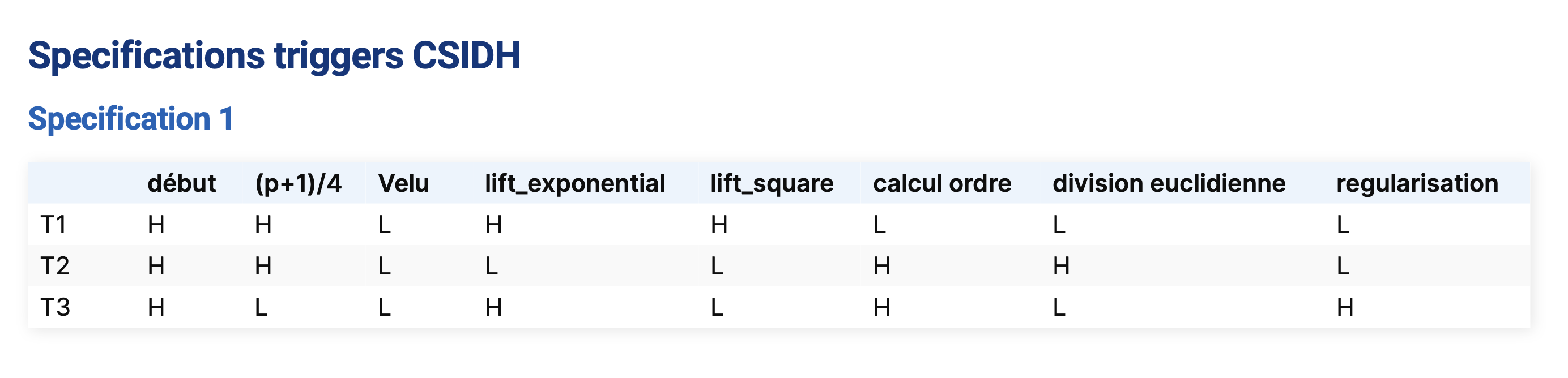
Par exemple, lorsque T1 est mesuré à 3.3 volts et que T2 et T3 sont à 0 volts, on est dans l’étape de calcul “lift_square”.

En superposant à notre signal une couleur pour chaque étape de calcul, on peut déjà y voir (un peu) plus clair :

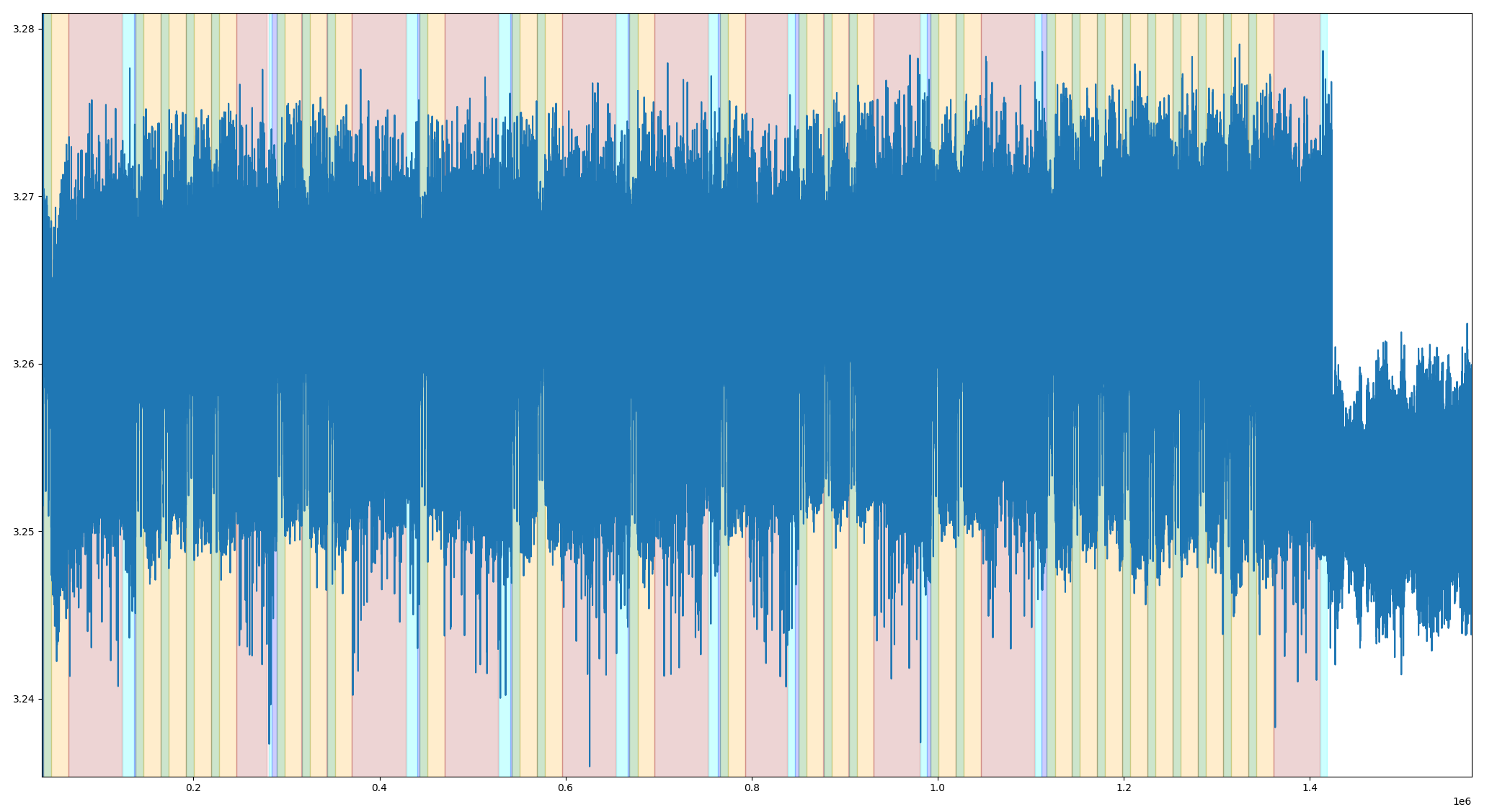
Pour comprendre ce qui se passe vraiment ici, on ne va pas y échapper : il va falloir étudier (un peu) le fonctionnement de CSIDH en commençant par regarder le code source en Rust qui nous est fourni. J’y ajoute le même code couleur que la capture ci-dessus pour que vous puissiez repérer les différentes étapes du calcul dans le code.

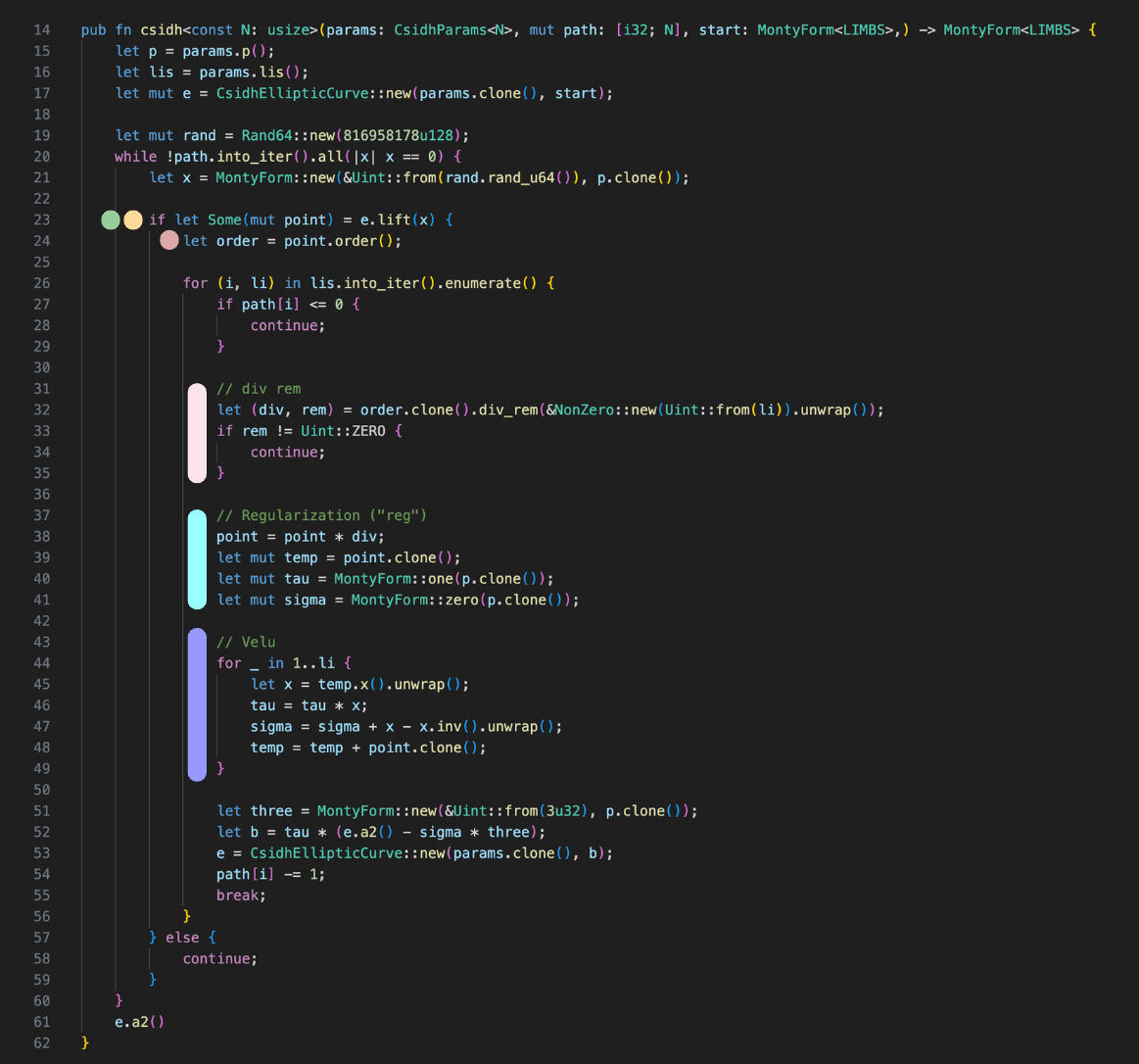
Dans notre version de CSIDH (ordre 419), on va effectuer 3 types d’opérations pour générer la clé (appelées isogénies) : les opérations de type 3, type 5 et type 7. Une clé privée est définie uniquement par le nombre d’isogénies de chaque type qui sont exécutées pour la créer. Par exemple, les isogénies 3,5,5,3,7,5 et 7,3,5,5,5,3 engendrent exactement la même clé privée.

Ainsi, une clé privée peut être définie par le nombre d’isogénies de chaque type utilisées pour la générer. Les deux clés de l’exemple précédent sont toutes deux définies par [2, 3, 1] puisqu’elles ont deux isogénies de type 3, trois isogénies de type 5 et une isogénie de type 7. Ce tableau caractéristique est passé au générateur dans le tableau path. Le tableau lis contient quant à lui les valeurs des isogénies, dans notre cas [3, 5, 7].

Pour mieux visualiser l’algorithme de génération de clés CSIDH, je l’ai représenté sous la forme d’un flowchart :

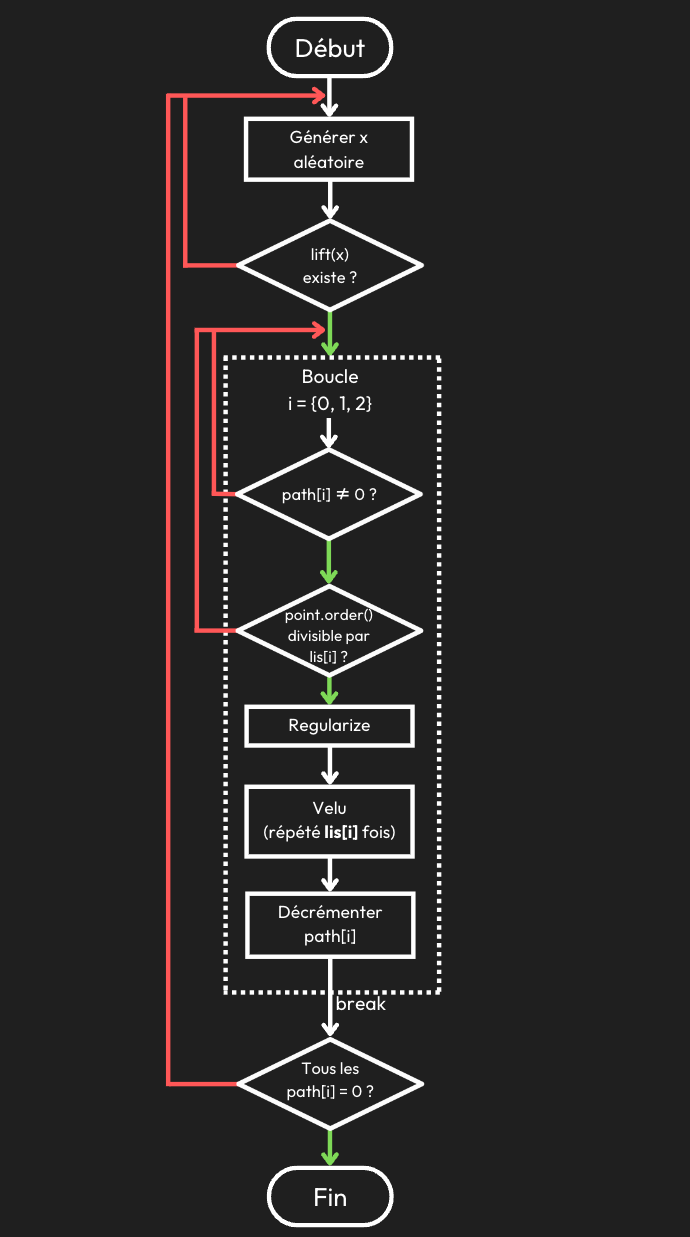
L’objectif du challenge 2/4 est de retrouver l’ordre des isogénies utilisées pour générer la clé privée de Bob. L’astuce se situe ici dans la répétition de l’opération Velu : elle sera répétée 3 fois dans le cas d’une isogénie 3, 5 fois pour une isogénie 5, et 7 fois pour une isogénie 7.

En supposant que l’opération Velu a un temps d’exécution relativement constant, on devrait donc voir apparaître des différences de durée de cette étape en fonction de l’isogénie exécutée. Sur les 10 cycles de Velu, voici les durées de cycle relevées par l’oscilloscope :

Début @ frame  137772 (durée 1945) - Velu
Début @ frame  289300 (durée 5442) - Velu
Début @ frame  442903 (durée 1945) - Velu
Début @ frame  542239 (durée 1938) - Velu
Début @ frame  668710 (durée 1943) - Velu
Début @ frame  766068 (durée 1946) - Velu
Début @ frame  850218 (durée 3700) - Velu
Début @ frame  992550 (durée 3694) - Velu
Début @ frame 1117367 (durée 5443) - Velu
Début @ frame 1418643 (durée 5442) - Velu

Ici, on voit clairement apparaître trois groupes de cycles Velu dont les durées approximatives sont de 1940 frames, 3700 frames, et 5440 frames. Ces groupes correspondent respectivement aux isogénies 3, 5 et 7.

À partir des durées de cycles Velu, on peut donc extraire la suite d’isogénies qui ont été exécutées : 3, 7, 3, 3, 3, 3, 5, 5, 7, 7.

On peut donc soumettre 404CTF{3733335577} pour valider la partie 2 et débloquer la partie suivante.

Partie 3/4

Pour le challenge 3 on doit à nouveau retrouver l’ordre des isogénies, mais cette fois-ci les triggers ne sont pas là pour nous aider à distinguer les différentes étapes du calcul. Cette fois, on va donc devoir trouver des motifs dans la courbe de consommation électrique pour faire le découpage.

Le signal brut (à gauche) est très difficile à traiter car il est bruité. J’applique donc un traitement (à droite) qui consiste à calculer le minimum, la moyenne et le maximum du signal sur chaque ensemble de 100 échantillons. Ça permet d’éliminer une grande partie du bruit, et aussi de diviser par 100 le nombre de points à afficher (la capture est très dense et fait ramer mon ordi, mais on n’a pas besoin d’autant de points pour distinguer les patterns).

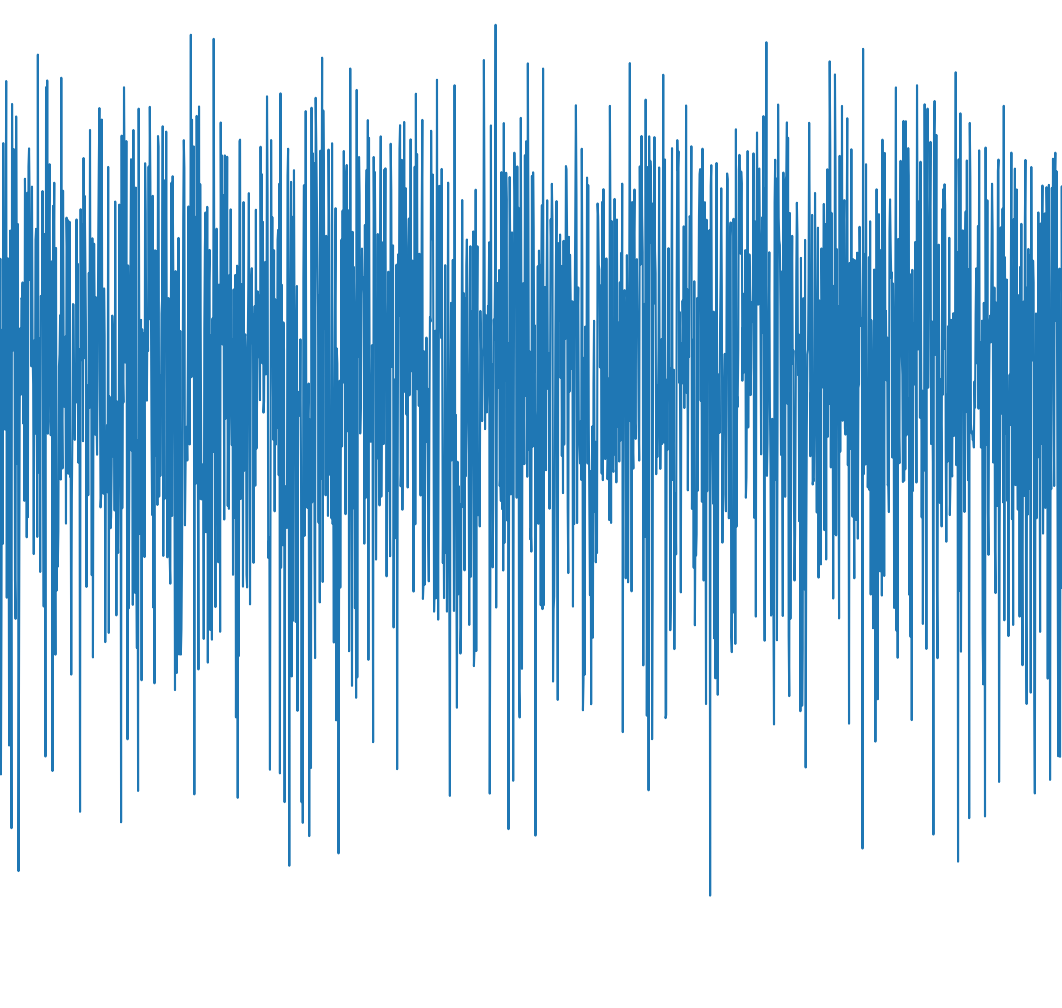
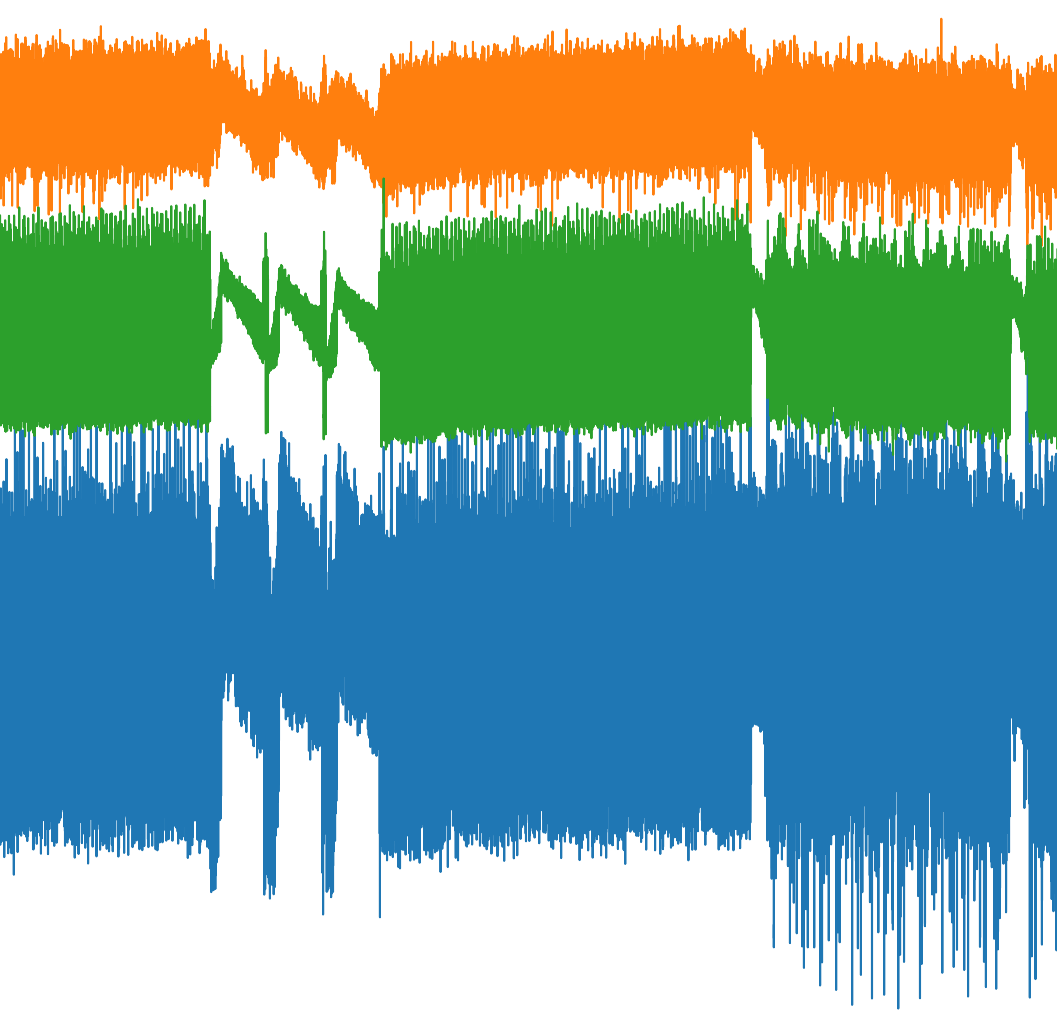
Sur la capture de droite ci-dessus, on peut voit plusieurs motifs très repérables. Plus particulièrement, celui qui comporte trois groupes décroissants était également visible lors de l’étape 2/4, et correspond au calcul de P+1/4. Ce groupe est très intéressant puisqu’il se trouve juste après la phase Velu qui nous avait permis de faire fuiter les isogénies utilisées.

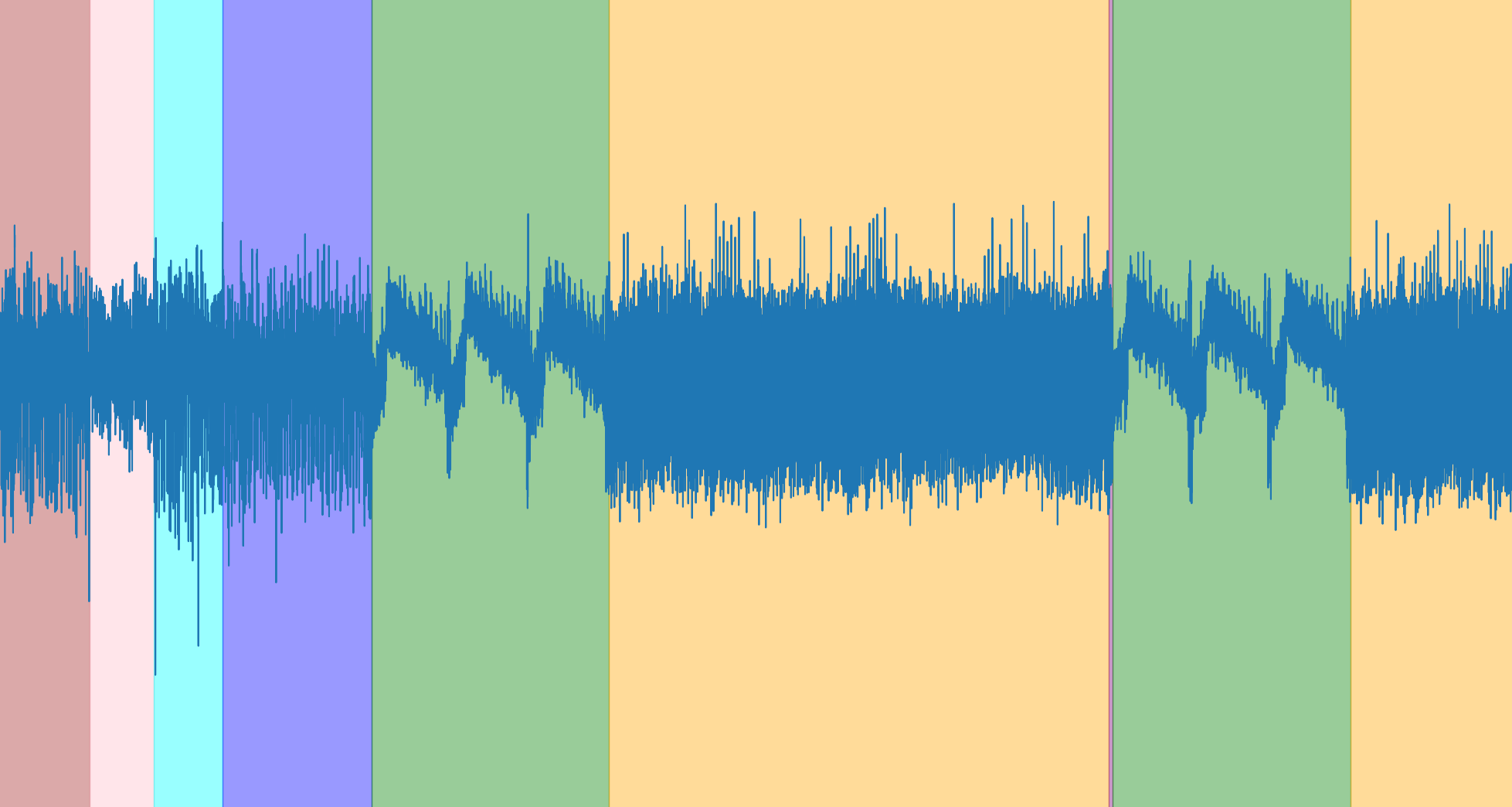
La durée du cycle Velu est difficile à mesurer puisqu’on ne voit pas bien la séparation entre celui-ci et la phase “régularisation” qui le précède (en bleu clair ci-dessus). Cependant, en regardant la forme de la courbe juste avant le début de la phase “P+1/4”, on distingue clairement deux groupes qui doivent donc correspondre à deux types d’isogénies différents. Je les note ici A et B (on remarquera que seulement deux des trois isogénies possibles sont utilisées dans la clé).

Comme les seules isogénies possibles sont 3, 5 et 7 et que le flag sera forcément au format 404CTF{ABBBABBABA}, ça nous fait seulement 6 flags possibles à essayer, le flag correct est 404CTF{5333533535}.

En pratique j’ai éliminé 3 de ces 6 possibilités en me basant aussi sur la durée de la division euclidienne qui était également très simple à visualiser sur la courbe, mais ce n’était pas nécessaire.

Partie 4/4

Pour la dernière partie du challenge, le code de la librairie Rust a été modifié pour nous compliquer la tâche. La boucle qui effectue les opérations Velu exécute désormais toujours 7 opérations, quelle que soit l’isogénie calculée : les isogénies 3 et 5 ajoutent des cycles artificiels qui n’ont pour seule utilité que d’engendrer un calcul en temps constant. D’autres modifications changent légèrement la forme de la trace, notamment la phase P+1/4 qui a une forme différente mais dont le motif reste très régulier et reconnaissable.

On va ici pouvoir utiliser la même technique que pour la partie 3, en étudiant la fin du cycle Velu. En effet, la forme de la courbe diffère que l’on soit dans une isogénie 3, 5 ou 7, même si la durée du cycle est maintenant la même.

On peut regrouper les 14 isogénies en 3 groupes distincts (indiqués ici A, B, C), qui nous donne à nouveau 6 flags possibles de la forme 404CTF{ABBBAAAAACCCCC}. On pouvait là encore élaguer les possibilités avec d’autres indices, notamment la durée de la phase de division euclidienne qui leak le nombre de divisions effectuées ou encore le fait que les isogénies de fin de liste ont également tendance à se retrouver en fin de calcul (ici C = 7).

Le flag attendu est 404CTF{35553333377777}, et me permet de finir cette série de challenges et marquer 3500 points, ce qui m’a donné une avance considérable sur le reste du scoreboard pendant plus d’une semaine avant que Thorn ne vienne nous rendre à tous un peu d’humilité.

J’ai passé environ 2 heures sur chaque partie (même la partie 1/4 que j’ai quand même implémentée correctement avant de découvrir qu’on pouvait tricher), le chall était vraiment agréable et m’a permis de découvrir CSIDH dont je n’avais jamais entendu parler :)

Je publierai certainement d’autres writeups de reverse et crypto cette semaine; n’hésitez pas à utiliser le formulaire de contact ci-dessous si vous avez une demande de writeup sur un challenge en particulier !