Nouveau top 100 mondial sur la Meta Hacker Cup - mes solutions

Sur le deuxième round du challenge Meta Hacker Cup, je me suis à nouveau classé dans le top 100 mondial !

Aujourd’hui, je vous présente les solutions aux 4 exercices de code comme je l’avais fait pour le round de qualification.

N’étant pas tout à fait d’accord avec les notes de difficulté attribuées par les organisateurs de Facebook, je vais présenter mes corrigés dans un ordre assez spécial : on va commencer tranquillement avec le A1, puis je laisse le A2 de côté pour y revenir à la fin de cet article.

On nous donne un paquet de cartes, numérotées de 1 à N sans doublons. L’objectif est de déterminer s’il est possible d’effectuer exactement K coupes du paquet pour parvenir à un ordre qui nous est fourni.

Pour rappel, une coupe d’un paquet de cartes, c’est ça :

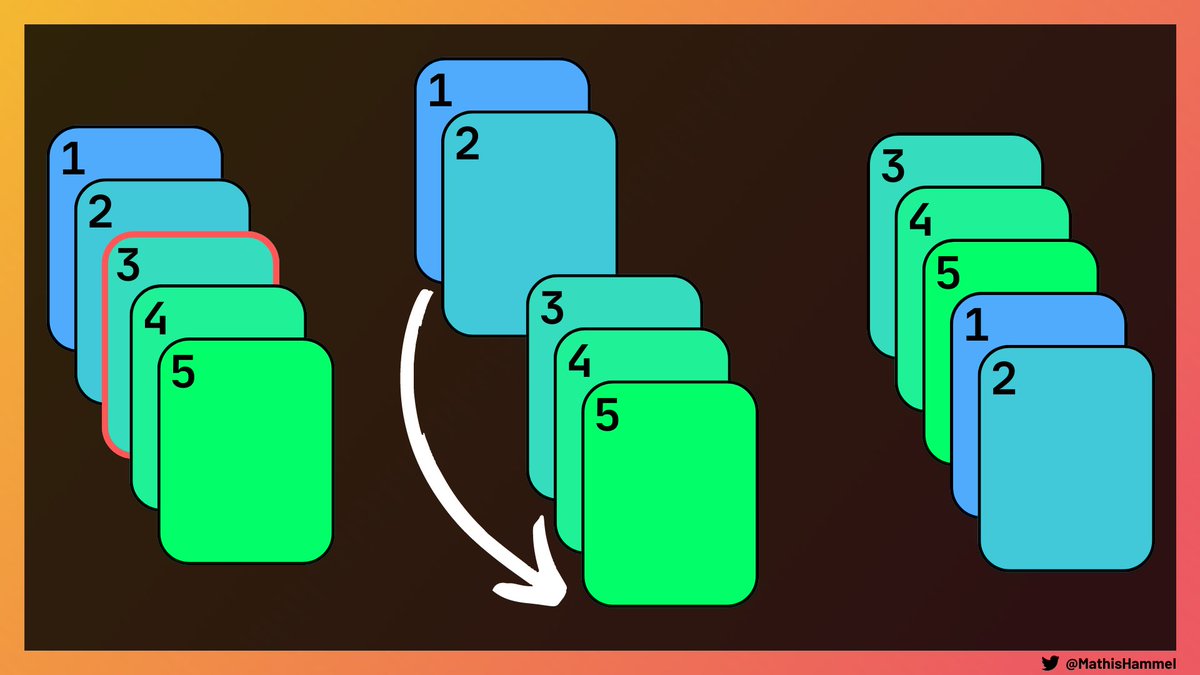
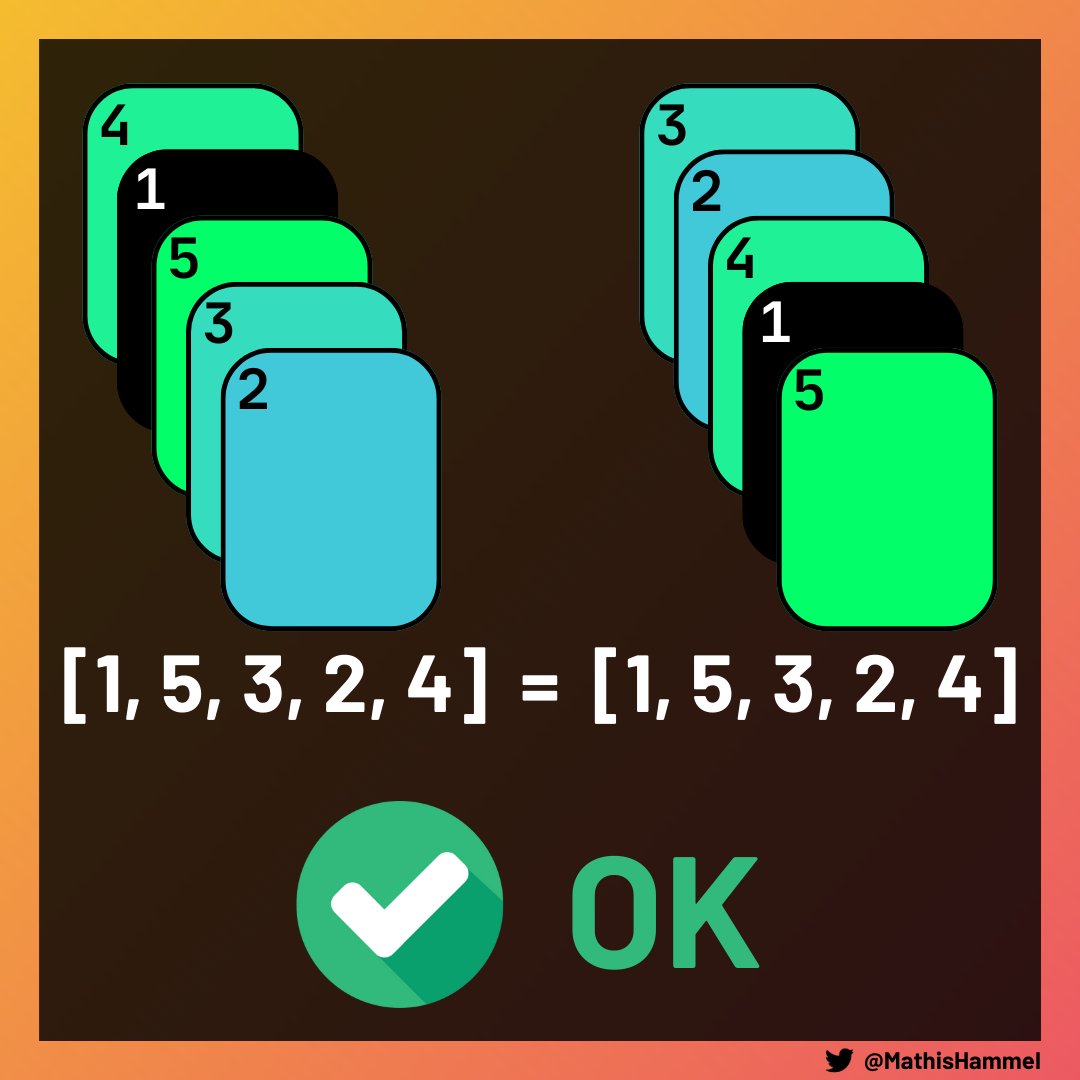
Prenons un exemple : on nous demande de passer de l’ordre [4, 1, 5, 3, 2] à [3, 2, 4, 1, 5] avec exactement deux coupes.

Il existe effectivement une solution que voici :

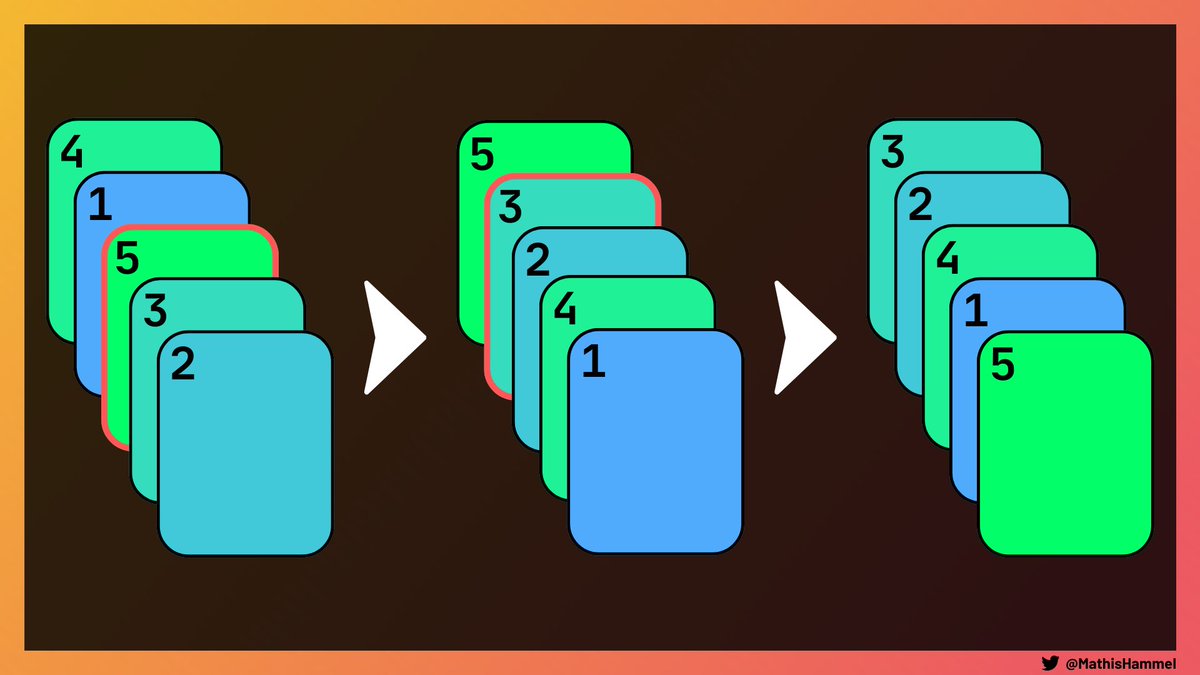
En revanche, passer de l’ordre [1, 2, 3, 4] à [4, 3, 2, 1] en 3 coupes est impossible.

En compétition de code, c’est toujours bien d’avoir des gadgets (cartes, dés, ciseaux) à portée de main en plus de son carnet de brouillons, pour comprendre plus facilement ce genre d’exos 😁

Après avoir compris l’énoncé et joué avec les cas d’exemple, la deuxième étape de la résolution d’un problème algorithmique est de chercher des propriétés intéressantes pouvant nous permettre de simplifier sa modélisation.

En continuant à jouer avec les cartes, on peut constater deux choses liées aux coupes.

Premièrement, on remarque qu’une coupe mélange très mal le paquet : en considérant que le paquet forme une boucle où la première et la dernière carte sont voisines, l’ordre ne change jamais !

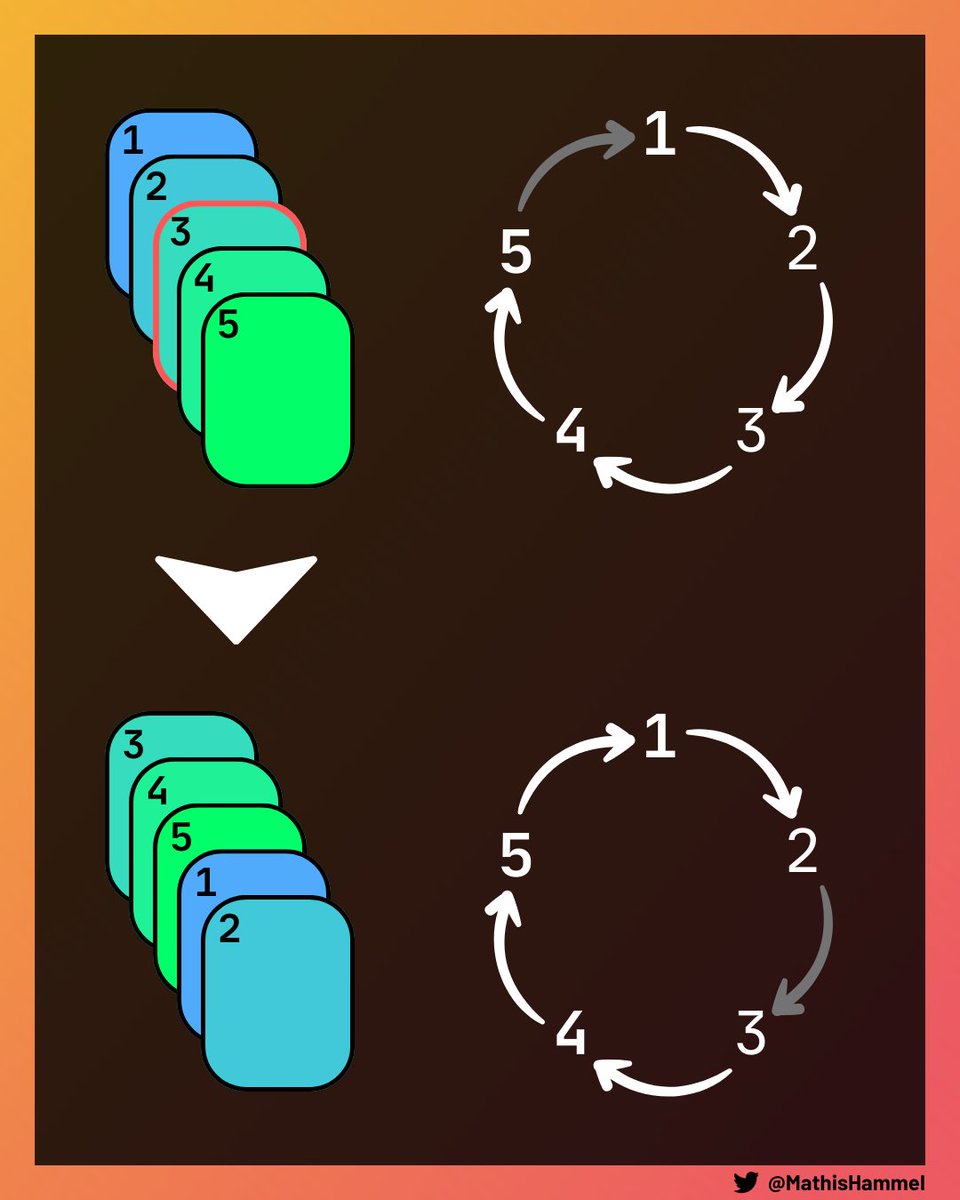
L’autre propriété remarquable est que plusieurs coupes successives (ici 2 cartes puis 1 carte) peuvent être réalisées en une seule coupe (ici 3 cartes).

De même, on peut diviser une coupe de X cartes en plusieurs coupes, tant que leur somme (modulo N) est égale à X.

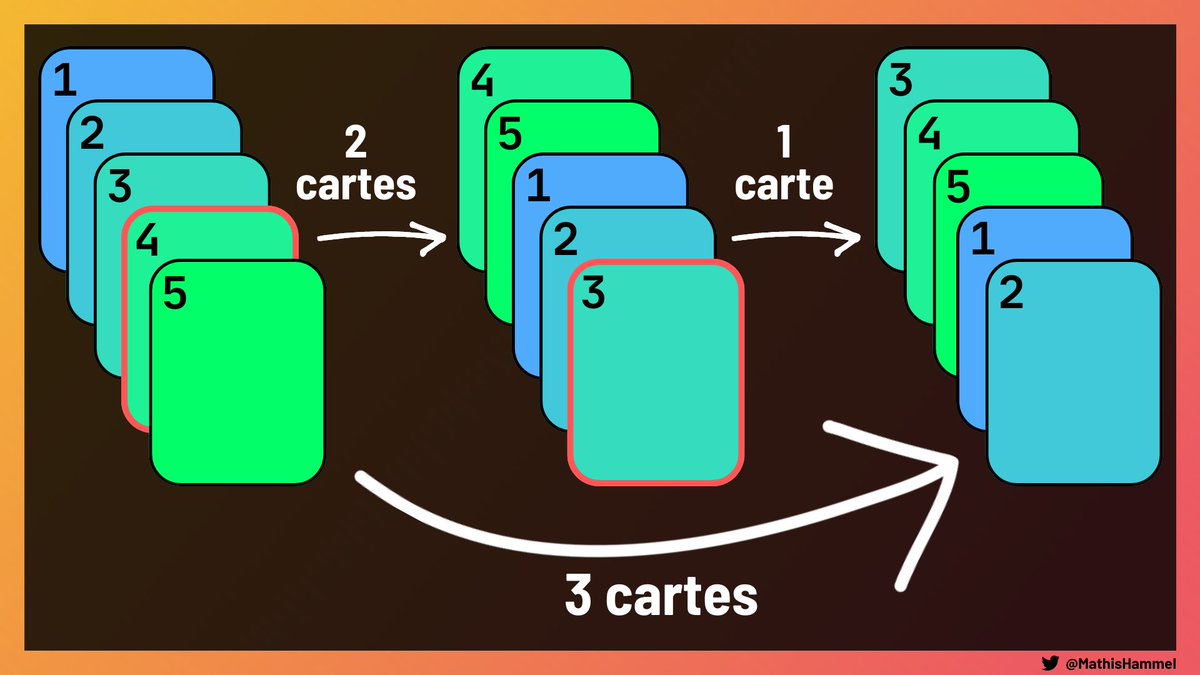
Le nombre de coupes imposé n’est donc pas important, car on peut les fusionner ou diviser à volonté pour obtenir le nombre d’actions désiré. À quelques exceptions près, on peut donc ignorer la valeur de K : il faut seulement déterminer si le mélange est réalisable en une coupe.

Pour savoir s’il est possible de passer d’un ordre à l’autre, il faut donc déterminer s’ils sont équivalents. On a vu qu’une coupe ne peut pas modifier fondamentalement l’ordre circulaire des cartes, elle ne fait que déplacer l’emplacement de la fin du paquet.

On sait donc qu’il est possible de passer d’un paquet à l’autre lorsque leurs cartes sont présentes dans le même ordre circulaire.

Pour déterminer ça algorithmiquement, il suffit de calculer l’ordre à partir de la carte 1 et voir s’il est identique entre les deux paquets !

Le code de vérification en Python est tout simple, on utilise l’opérateur de slicing pour mettre la valeur 1 en premier dans chaque liste.

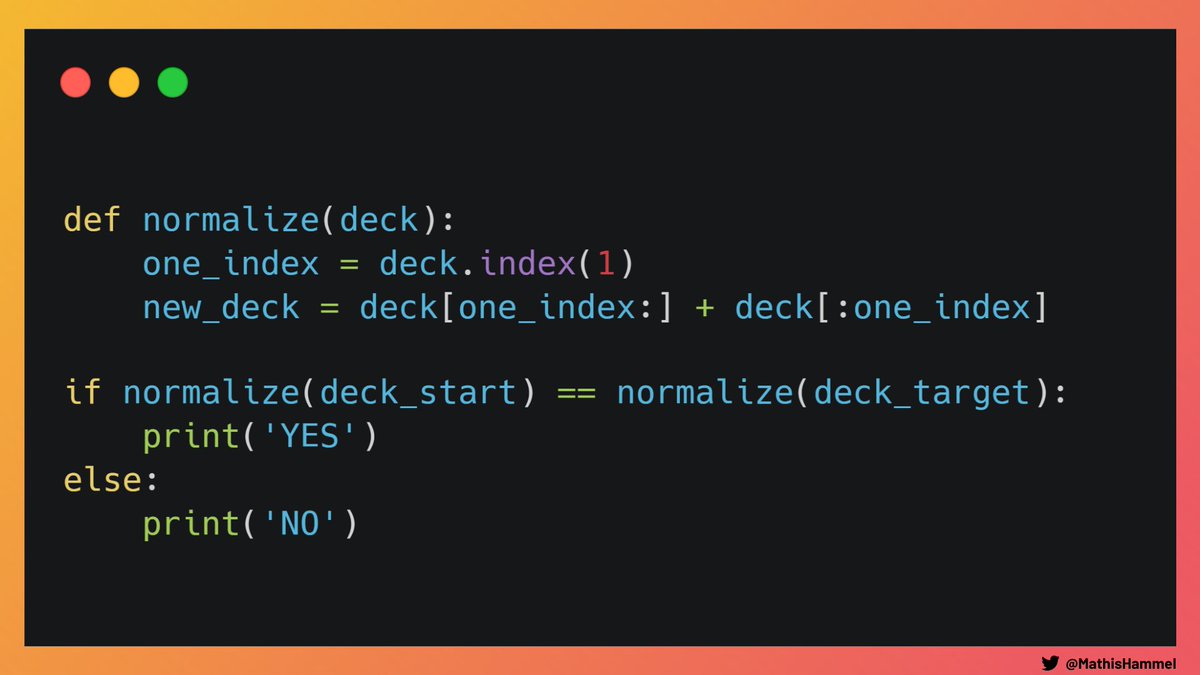
Il reste néanmoins quelques cas particuliers à traiter, le moindre oubli pouvant être très coûteux sur cette compétition : si on donne la moindre réponse incorrecte parmi les 80 tests, c’est 0 points.

Et en plus de ça, on n’a le droit qu’à une unique soumission !

On a trois cas particuliers pour lesquels le code ci-dessus donne une mauvaise réponse. Voici des contre-exemples qui correspondent :

• [1, 2, 3] -> [2, 3, 1] en 0 coupe
• [1, 2, 3] -> [1, 2, 3] en 1 coupe
• Je vous laisse trouver le dernier 😉 (indice : 2 cartes)

On reviendra plus tard à la deuxième moitié de ce problème, où chaque carte peut être présente en plusieurs exemplaires.

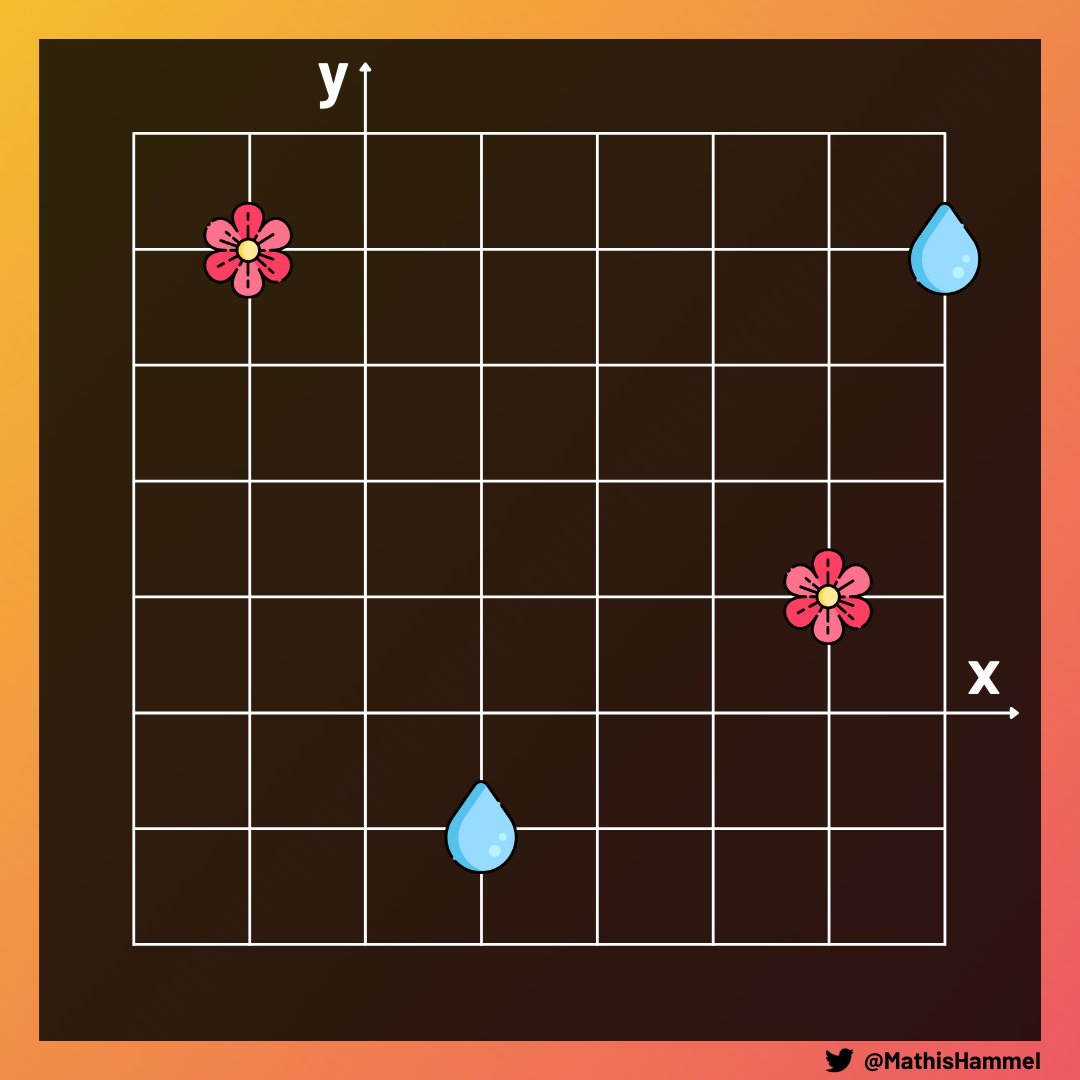
Dans le deuxième exercice, on nous fournit un plan où figurent des puits et des plantes. L’objectif est de calculer un “score d’irrigation”.

Le calcul de ce score est simple : pour chaque paire puits/plante, on va calculer le carré de la distance qui les sépare. Le score correspond à la somme de tous ces carrés.

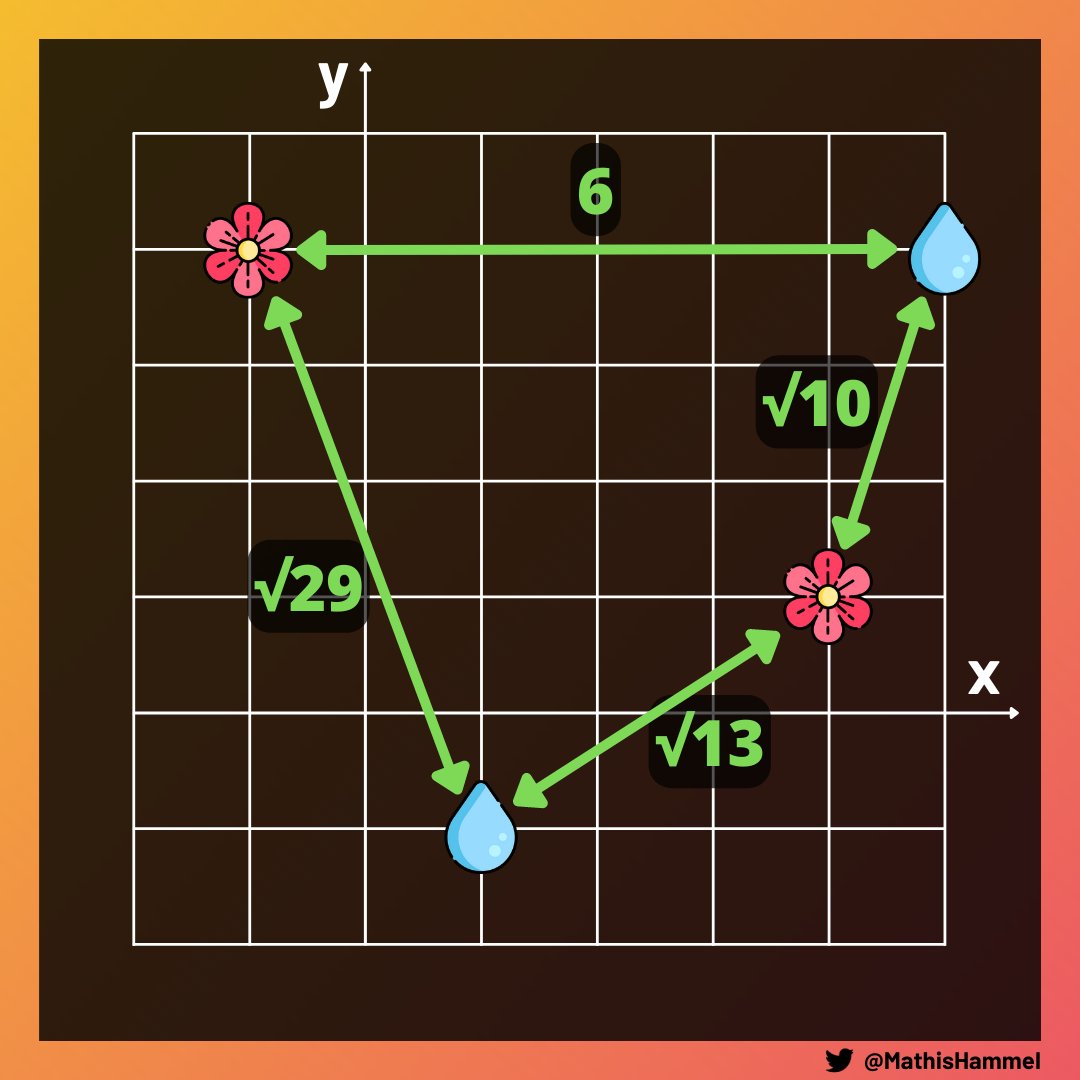
Par exemple ici, nos 4 paires ont des distances respectives de 6, √29, √10 et √13 (obtenues grâce au théorème de Pythagore).

En additionnant les carrés de ces distances, on obtient donc 36+29+10+13, soit un score de 88 qui sera la réponse au problème.

Alors ce problème, il a l’air vraiment très simple : deux boucles pour itérer sur les arbres et les puits, un calcul des distances et c’est réglé !

En faisant ça, on va rapidement être confrontés à un problème de performance : l’énoncé nous informe qu’il est possible d’avoir jusqu’à 500.000 arbres et 500.000 puits.

Avec sa complexité de O(N²), l’algorithme naïf prendrait plusieurs heures pour ce calcul 😖

Il va nous falloir trouver une optimisation qui permet de faire le calcul de score en quelques millisecondes.

Ici, l’astuce va être purement mathématique : certaines opérations sont répétées un grand nombre de fois dans l’algorithme précédent, et on va pouvoir les condenser.

Accrochez-vous un peu sur les 3 prochaines minutes, la notation mathématique peut faire peur mais c’est du niveau terminale (et au pire vous skippez, c’est pas très grave).

On va d’abord calculer le score entre UN SEUL puits et toutes les plantes, avec la formule de Pythagore :

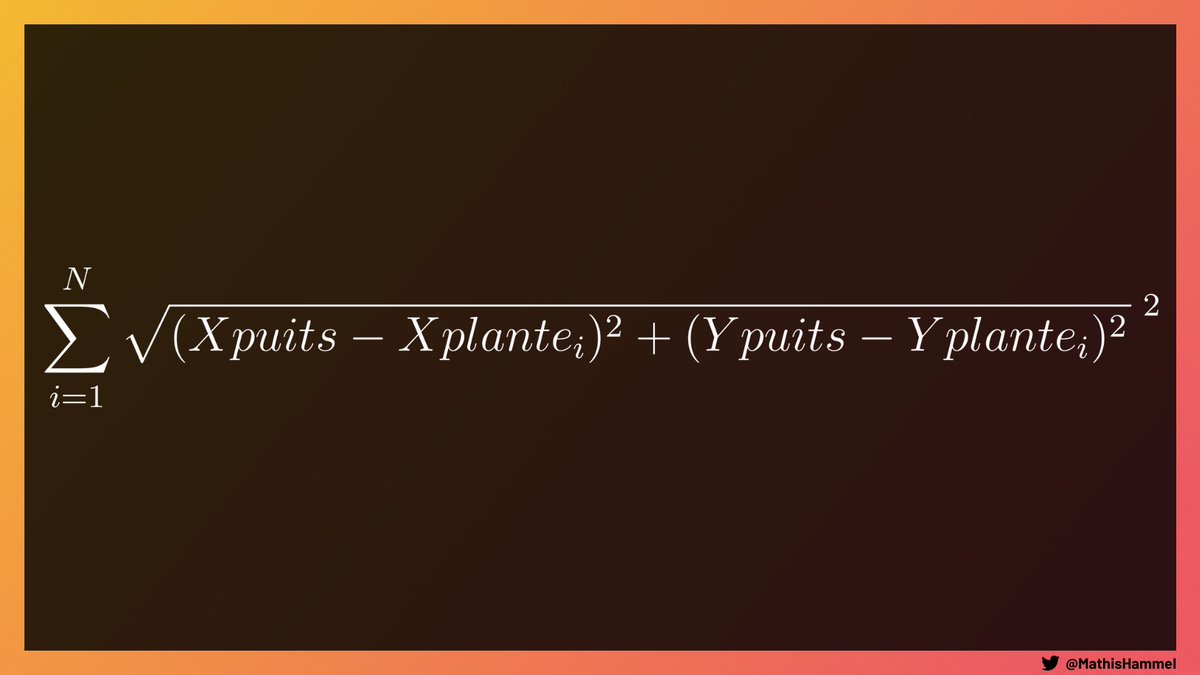
La première simplification que l’on peut faire, c’est d’éliminer le combo carré + racine carrée qui s’éliminent mutuellement.

Avec ça, on peut voir que les deux composantes X et Y peuvent être calculées indépendamment.

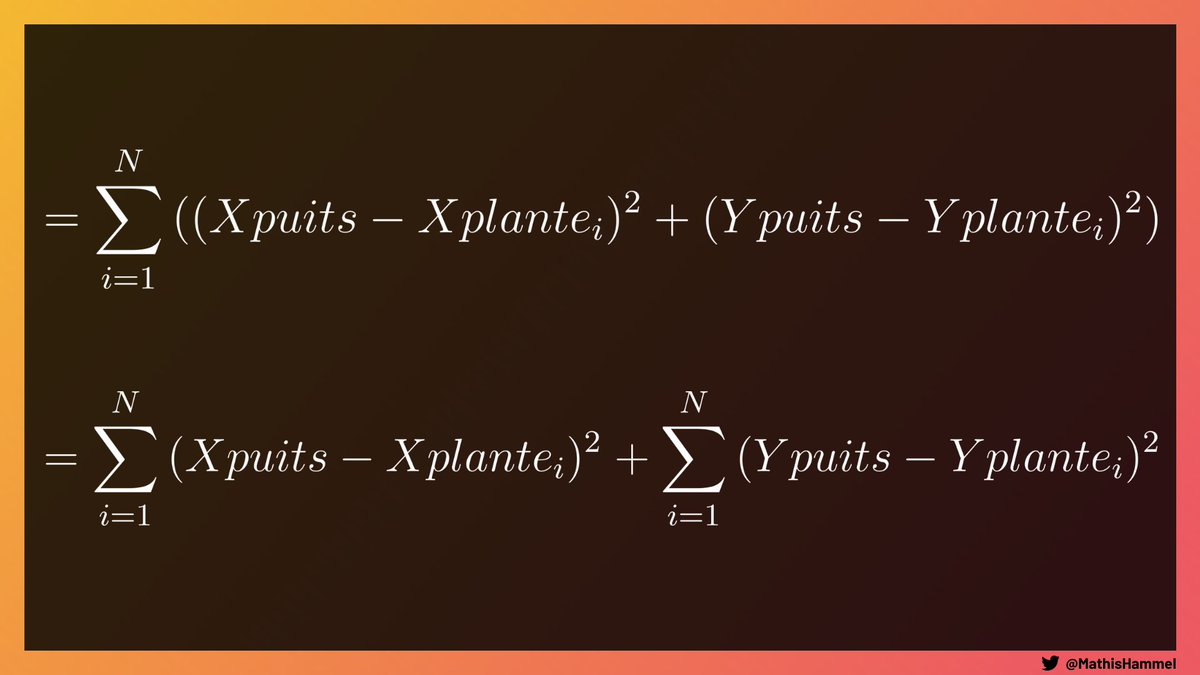
Pour simplifier la suite, on va garder uniquement le calcul du score sur la composante X, le score selon Y sera calculé pareil.

Grâce à l’identité remarquable (a-b)² = a² - 2ab + b², on peut développer la formule :

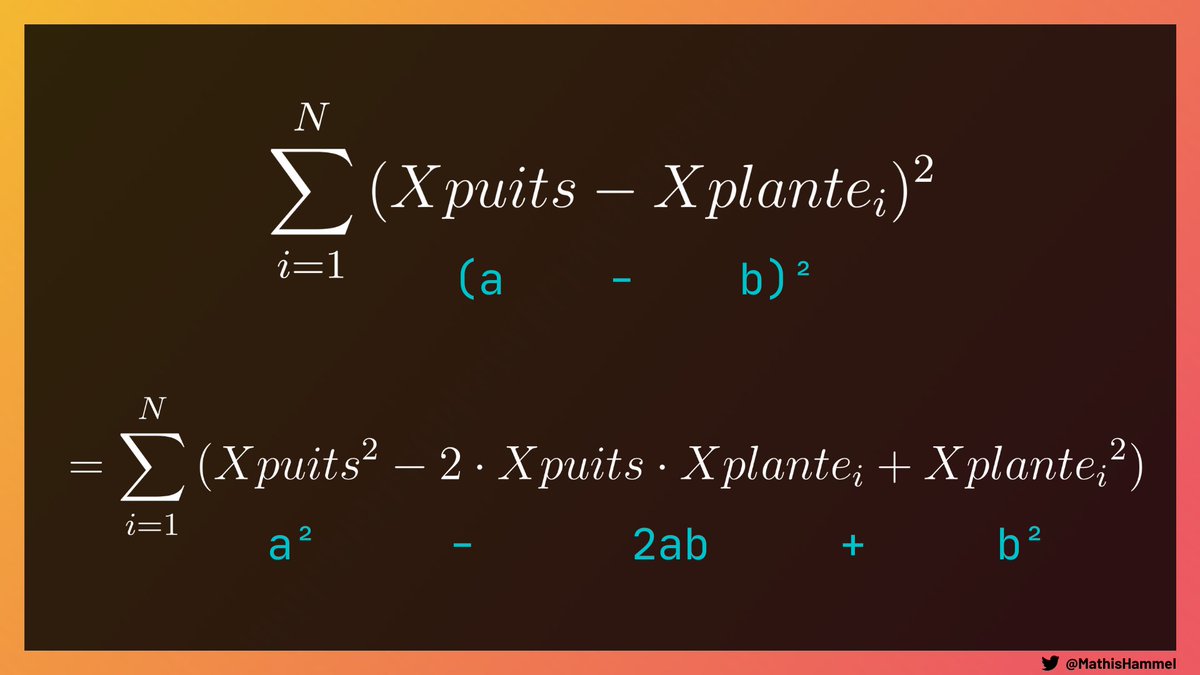
Ici encore, on peut séparer cette somme en trois sommes indépendantes :

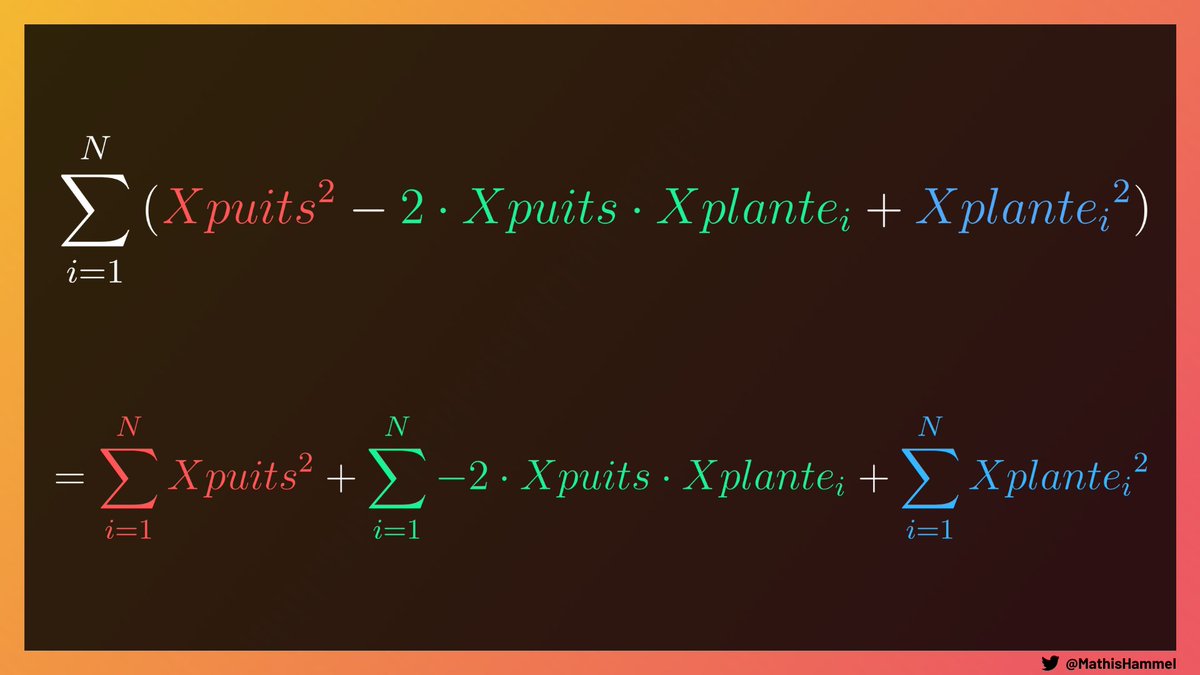
Et enfin, la dernière étape de notre optimisation, celle qui va décorréler les puits et les plantes dans notre calcul.

On rappelle ici qu’on est en train de calculer le score pour un seul puits, la valeur Xpuits est donc une constante dans notre formule.

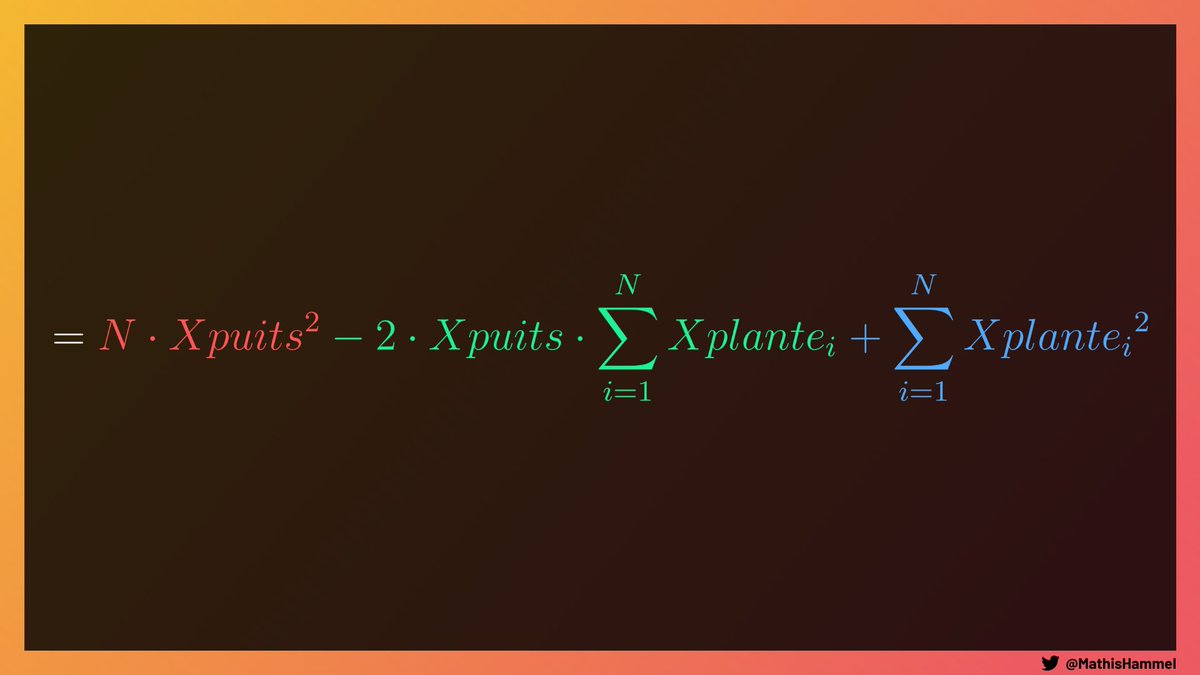
Mais il nous reste un gros problème : la formule contient encore des sommes, donc le calcul de chaque puits doit parcourir la liste de toutes les plantes !

En réalité non, car ces deux sommes sont les mêmes pour chaque puits. On peut donc les précalculer une fois pour toutes.

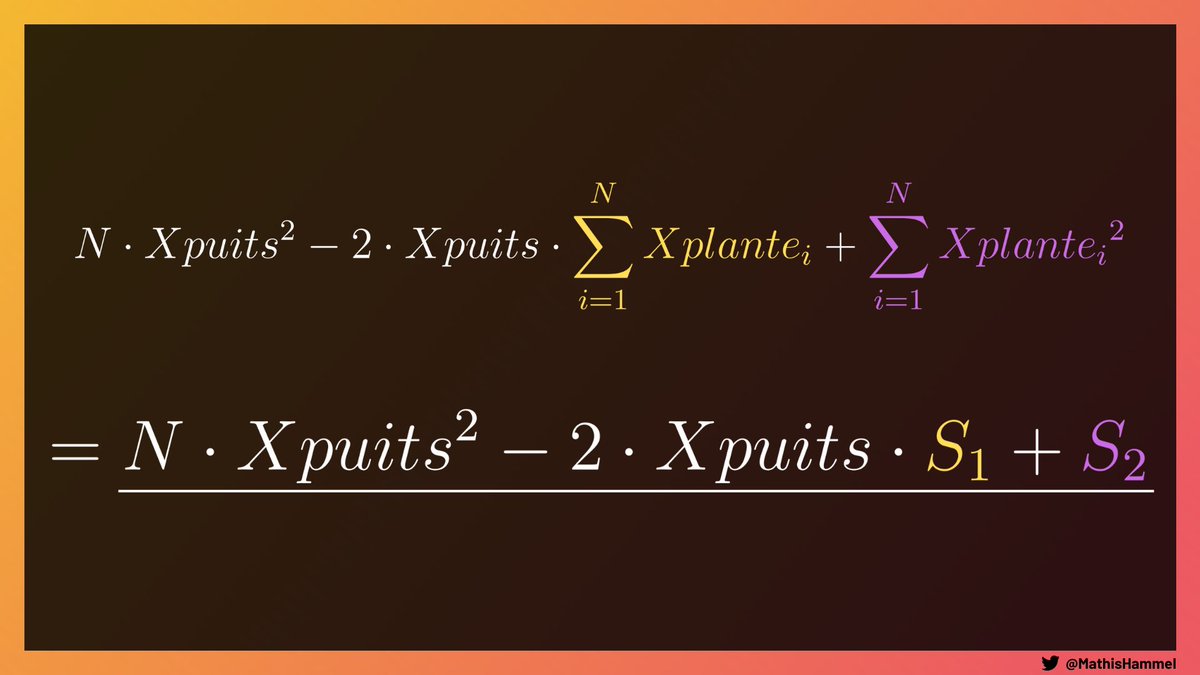
On peut donc maintenant calculer le score d’un puits avec une complexité O(1) alors qu’elle était O(N) précédemment, ce qui nous permet de calculer le score total des N puits en complexité O(N) au lieu de O(N²) 😁

Voici le code :

Revenons maintenant à la deuxième moitié du problème A (celui avec les jeux de cartes), que j’ai décidé de traiter en dernier car il fait appel à une notion d’algorithmique avancée.

Souvenez-vous de l’exercice A1, pour savoir s’il est possible de passer d’un deck à l’autre il suffisait de déterminer si les cartes étaient dans le même ordre circulaire entre le départ et l’arrivée.

Ici c’est exactement la même chose, mais les cartes peuvent apparaître plusieurs fois. Notre normalisation qui remet la carte 1 au début de la liste ne marche plus !

Prenons cet exemple où le code donnera une mauvaise réponse (les decks sont bien dans le même ordre) :

On peut essayer de corriger notre algo de normalisation pour gérer le cas où on a plusieurs cartes 1, mais on se retrouvera toujours dans des impasses où le code est soit incorrect, soit trop lent.

Pour vérifier si deux ordres circulaires sont identiques, au lieu d’essayer de les normaliser on peut simplement essayer les N rotations possibles et voir si on trouve une correspondance.

Cet algorithme est correct mais trop lent.

Mais on peut en réalité accélérer la comparaison. Imaginons qu’il existe une fonction de hachage capable de condenser un tableau en une valeur unique.

Au lieu de comparer tous les ordres possibles, il suffirait de comparer leurs hashs :

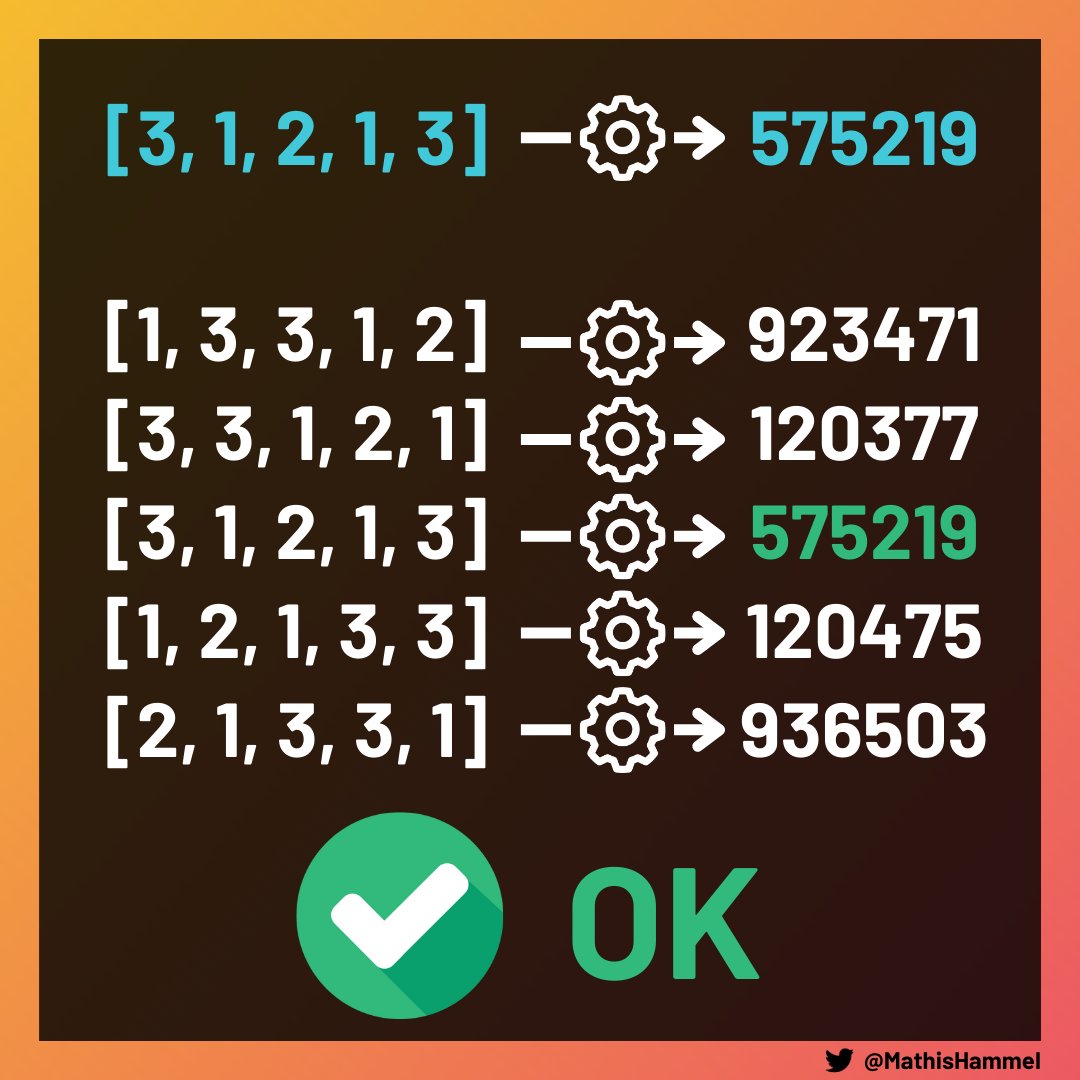
Le souci, c’est qu’une fonction de hachage doit forcément prendre en compte les N éléments de la liste, ce qui est incompatible avec la complexité O(1) désirée pour son calcul.

En fait, c’est tout à fait possible avec un peu d’astuce !

Considérons que notre calcul de hash prenne la forme suivante, en se basant sur les puissances d’un nombre, prenons ici 31 pour l’exemple (fun fact : c’est exactement comme ça que fonctionne hashCode en Java)

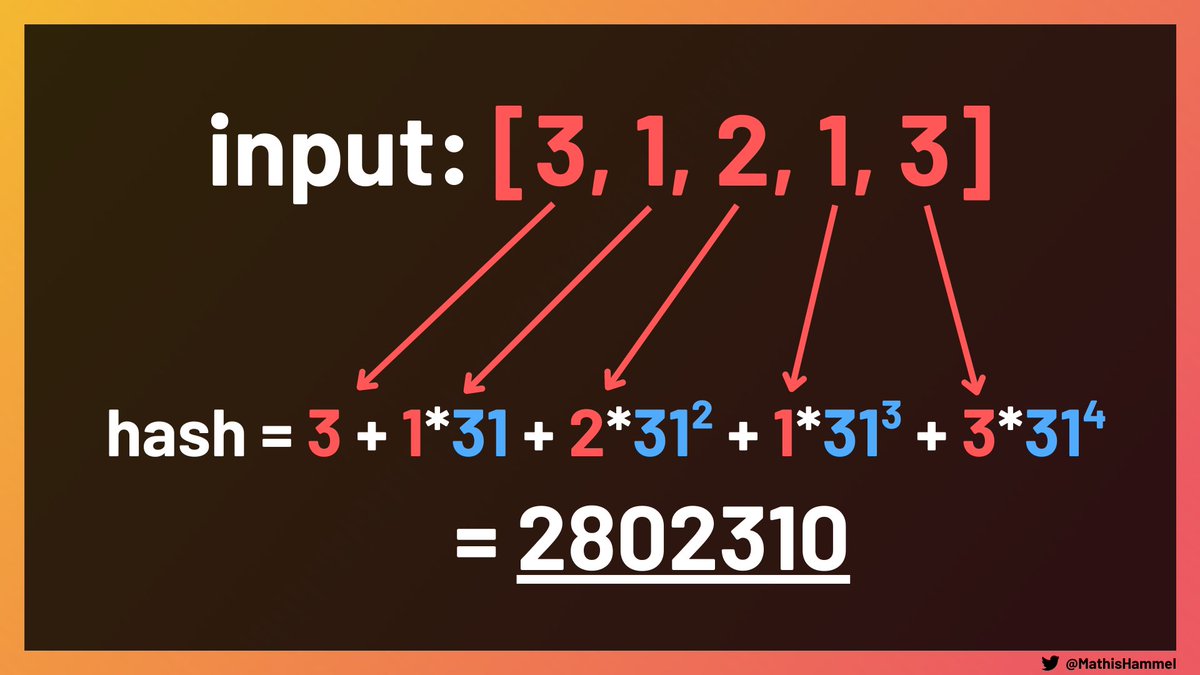
Si on souhaite ajouter un élément à la fin de notre liste, il n’est pas nécessaire de tout recalculer : la différence entre les deux hashs dépendra seulement de la valeur du nouvel élément et de la taille du tableau.

Pour retirer le premier élément, pareil : on soustrait sa valeur au hash puis on divise par 31, ce qui permet de recalculer le hash sans reparcourir toute la liste.

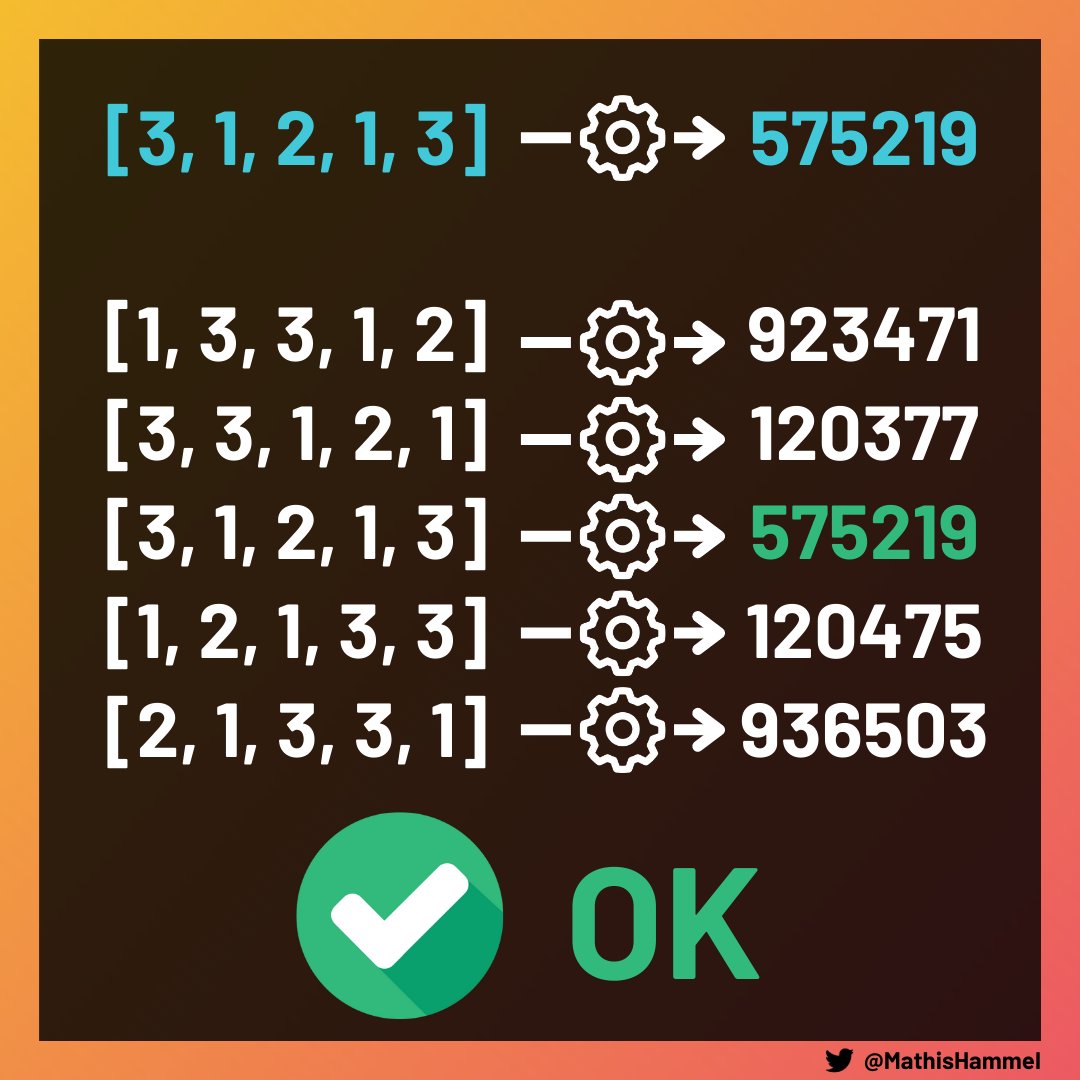
En faisant ces deux opérations successivement, vous voyez qu’on a réussi à calculer le hash de [1, 2, 1, 3, 3] à partir de celui de [3, 1, 2, 1, 3] avec une complexité O(1). En répétant l’opération, on peut calculer les hashs de toutes les rotations très rapidement !

Il restait sur ce round un problème très difficile que je n’ai pas pu résoudre, mais comme très peu de personnes l’ont validé je suis quand même classé 90e mondial 😁

Le prochain round commence dans quelques minutes et dure jusque 22 heures, vous pouvez suivre ma progression ici.

Je dois terminer dans le top 2000 pour recevoir le T-shirt de cette édition, et top 500 pour me qualifier au prochain !

Et pour retrouver le post précédent qui portait sur le round de qualification, c’est par ici.

Comme d’habitude, n’hésitez pas à partager mon travail si ça vous a plu, qu’un article comme celui-ci me prend environ 2 jours de travail entre l’écriture et les illustrations.

Update : jme suis fait détruire sur le round 3, 1312e 😭

J’étais vraiment pas loin de décrocher le top 500 mais il m’a manqué une optim et un debug pour quadrupler mon score. On se contentera du t-shirt, à l’année prochaine !